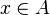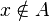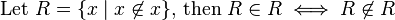doronshadmi
Penultimate Amazing
- Joined
- Mar 15, 2008
- Messages
- 13,320
Let's start with what you still do not get.let's start with what you got right.
Any given set exists as an abstract mathematical object, whether it does or does not have members.
The notion of this abstract existence (which is inaccessible to the abstract existence of its members) is notated by the outer "{" and "}".
In other words, no matter how many members a given set has, they are inaccessible to the abstract level of existence of the set (where this inaccessible level is notated by the outer "{" and "}").
If you are able to understand what is written above, then you have no problems to understand the following:
|{}|=0 , |{{}}|=1 |{{},{{}}}|=2 etc. , or |{{}, {{}}, {{},{{}}}, ... }| < aleph0 exactly because the level members is inaccessible to the level of being a set, where the abstract notion of being a set is notated by the outer "{" and "}" (where aleph0 is at the level of being a set).
So, the level of (abstractly) existing members is no more than potential infinity w.r.t (abstractly) actual infinity at the level of being a set, where "|{{}, {{}}, {{},{{}}}, ... }| < aleph0" is the exact abstract mathematical expression of this notion (the abstract notion of the difference between potential infinity and actual infinity).
By using only verbal_symbolic expressions for sets (for example: Ø , S , N etc.) one simply misses the abstract notion of the difference between potential infinity and actual infinity.
Last edited: