Cont: Deeper than primes - Continuation 2

Status
Not open for further replies.

doronshadmi

Penultimate Amazing
doronshadmi
Joined
Mar 15, 2008
Messages
13,320
Posted By: zooterkin


jsfisher said:
False and false. That there is no element in an infinite sequence with infinitely many segments is independent of the sequence's cardinality.
Click to expand...


|N| folded line segments does not mean that one of the folded line segments has |N| sub-segments.

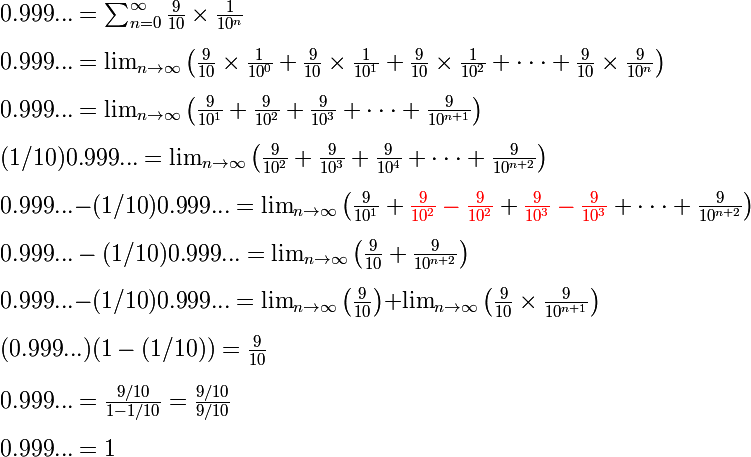
For example, in the case of Koch Fractal the formula is (X/4J)*4J, where j=1 to |N|, such that if j = |N|, this is exactly the case that enables to extend (to go beyond) all the cases of finite sub-segments, in order to get X in the case of 2*(a+b+c+d+...) (this is exactly |N| observation).

This is not the case if X is observed from |R|, exactly because |N| extension < lR|, and we need |R| extension in order to get X.

Please look again very carefully at http://www.internationalskeptics.com/forums/showpost.php?p=10316119&postcount=4298.
 
Last edited by a moderator:
jsfisher said:
Then perhaps, just this once, you should consider defining your terms.
Click to expand...

If you read all of
doronshadmi said:
There are |N| folded line segments because the cardinality of the sequence <41,42,43,...> (which is the number of sub-segments at each degree of Koch Fractal) is |N|).
Click to expand...
you are easily realize that |N| is not one of numbers of sub-segments in any degree of Koch Fractal (or in other words there are |N| values in sequence <41,42,43,...> but no one of them is 4|N|).

jsfisher, mathematical expressions like n = 1 to ∞ are used, isn't it?

I simply refine ∞ by distinguish between |N| and |R|.
 
Last edited:
doronshadmi said:
If you read all of

you are easily realize....
Click to expand...

You overrate your power of expression with clarity.

Be that as it may...

You have a (countably infinite) sequence of values that has a limit of a value. The cardinality of the set of reals is irrelevant to this.

On the other hand, if you want to take a line segment view of the process, you have a (countably infinite) sequence of line segments that collectively span a line segment. All of the line segments involved have the same "number" of points, but, again, the cardinality of the continuum is not relevant.

Instead, rather than staying consistent, you switch midway to conflate the two and view the resulting confusion as revelation.
 
Last edited:
jsfisher said:
... the cardinality of the continuum is not relevant.
Click to expand...
It is relevant.

You arbitrarily force |N| as the only possible option to obverse the real-line.

jsfisher said:
you switch midway
Click to expand...
I do not switch midway, on the contrary, I show two different cases that depend of two different observations, as follows:

1) By using |N| observation of the real-line 2*(a+b+c+d+...)=X.

2) By using |R| observation of the real-line 2*(a+b+c+d+...)<X.
 
Last edited:
doronshadmi said:
It is relevant.

You arbitrarily force |N| as the only possible option to obverse the real-line.
Click to expand...

I did? I don't recall that.

Be that as it may, what does that have to do with a (countably) infinite sequence having a limit?
 
jsfisher said:
I did? I don't recall that.

Be that as it may, what does that have to do with a (countably) infinite sequence having a limit?
Click to expand...

Series 2*(a+b+c+d+...) is based on the convergent sequence <a,b,c,d,...> of |N| values.

2*(a+b+c+d+...)=X by define X as the limit of 2*(a+b+c+d+...), as follows:

|N|+1 = |N| (where this +1 is exactly the way that is used to define X as the limit of 2*(a+b+c+d+...)).

By using the fact that |N|+1 = |N| you can conclude that 2*(a+b+c+d+...)=X.

But this little trick does not work from |R| observation of the real-line simply because |N|+1 = |N| < |R|.
 
Last edited:
doronshadmi said:
Series 2*(a+b+c+d+...) is based on the convergent sequence <a,b,c,d,...> of |N| values.
Click to expand...

Please stop trying to use |N| as an ordinary number. The sequence has the same cardinality as the set of natural numbers.

...continued attempts to introduce the continuum where it doesn't belong snipped...
Click to expand...
 
jsfisher said:
Please stop trying to use |N| as an ordinary number. The sequence has the same cardinality as the set of natural numbers.
Click to expand...

The sequence has |N| values, which is the same cardinality as the set of natural numbers that also have |N| values (natural numbers, in this case).

You arbitrarily continue to ignore |R| as the cardinality of the real-line, which is inaccessible to your |N|+1 trick.
 
Last edited:
Ok, now let's go beyond the real-line in order to deal with the tower of power line.

It goes like this:

Between any two natural numbers along the tower of power line, there are |N| rational numbers.

Between any two rational numbers along the tower of power line, there are |R| irrational numbers.

Between any two irrational numbers along the tower of power line, there are |P(R)|_numbers.

Between any two |P(R)|_numbers along the tower of power line, there are |P(P(R))|_numbers.

...

etc. ... ad infinitum, where the inaccessible limit of the tower of power line is simply the non-composed 1-dimesional space.
 
doronshadmi said:
You arbitrarily continue to ignore |R| as the cardinality of the real-line
Click to expand...

How, exactly, is the cardinality of the real numbers in any way relevant to the valuation of a convergent series? So far, you have not shown any connection whatsoever. Nor have you show in any way that it would in any way impact the valuation of a convergent series.
 
doronshadmi said:
So far you are using at most |N| observation of the real-line.
Click to expand...

Did I? Where?

Meanwhile, back to where we were not discussing the real line at all, but the valuation of a convergent series, how is the cardinality of the real numbers relevant?
 
doronshadmi said:
You are free to go back, but in that case all you do is not a nice dodge from the real-line.
Click to expand...

A double-dodge. now.

Meanwhile, back to where we were not discussing the real line at all, but the valuation of a convergent series, how is the cardinality of the real numbers relevant?
 
Last edited:
doronshadmi said:
http://www.internationalskeptics.com/forums/showpost.php?p=10319593&postcount=4318

http://www.internationalskeptics.com/forums/showpost.php?p=10318701&postcount=4312
Click to expand...

If those posts addressed my question, I won't need to repeatedly ask it. The question was:

Meanwhile, back to where we were not discussing the real line at all, but the valuation of a convergent series, how is the cardinality of the real numbers relevant?

And for the sake of context and example, the series represented by 0.999... is the reference.
 
jsfisher said:
And for the sake of context and example, the series represented by 0.999... is the reference.
Click to expand...
http://www.internationalskeptics.com/forums/showpost.php?p=10306748&postcount=4282 and http://www.internationalskeptics.com/forums/showpost.php?p=10316119&postcount=4298 deal with the same reasoning, which is |N| and |R| observations of the real-line.

This time please do not ignore the details of http://www.internationalskeptics.com/forums/showpost.php?p=10318337&postcount=7 and http://www.internationalskeptics.com/forums/showpost.php?p=10318659&postcount=9.

In other words, there is no
jsfisher said:
back to where we were not discussing the real line at all.
Click to expand...


It is up to you to decide if you wish to continue the discussion on |N| and |R| observations of the real-line.

(http://www.internationalskeptics.com/forums/showpost.php?p=10318701&postcount=4312 goes beyond the real-line).
 
Last edited:
doronshadmi said:
...non-response snipped...
Click to expand...


Doron, you have yet to show how the valuation of 0.999... invokes the continuum.

Hand-waving at snowflakes doesn't help. Asserting the reals are not complete does the exact opposite of help.
 
jsfisher said:
Asserting the reals are not complete does the exact opposite of help.
Click to expand...
The reals are complete (they have exactly |R| number of values along the tower of power line) but it does not mean that |R| is the biggest cardinality along the tower of power line.

Please stop ...snipping... if you really wish to continue our discussion.

Thank you.
 
Last edited:
doronshadmi said:
Mathematical expression like n = 1 to ∞ is indeed hand-waving of the concept of Infinity.
Click to expand...

Huh? How else would you note down an enumeration from 1 to ∞?

And what has an enumeration to do with the concept of infinity (notice, no capital I, it is not a deity or some shady woo-concept).

Infinity is really, really simple; it has no end; 'In' as in 'the opposite of' and 'fin' as in 'end'.

Literally it means endless. How hard can this be?
 
Doron, you have yet to show how the valuation of 0.999... invokes the continuum.
 
jsfisher said:
Doron, you have yet to show how the valuation of 0.999... invokes the continuum.
Click to expand...
All you have to do is to observe 0.999... (which is an |N| thing) from |R|.

jsfisher, your are an essential factor to show how the valuation of 0.999... invokes the continuum.

As long as you exclude yourself, you simply can't observe it.
 
doronshadmi said:
All you have to do is to observe 0.999... (which is an |N| thing) from |R|.
Click to expand...

All you have to do, then, is explain how this gibberish is semantically intelligible, and how the continuum is invoked for the valuation of 0.999..., and how any of this has to do with Mathematics.

ETA: Hint: "observe...from |R|".
 
Last edited:
jsfisher said:
All you have to do, then, is explain how this gibberish is semantically intelligible, and how the continuum is invoked for the valuation of 0.999..., and how any of this has to do with Mathematics.
Click to expand...

You still exclude yourself as an essential factor of |R| observation of the real-line.

Without your |R| observation of the real-line, you simply unable to know why 0.999... (which is an |N| thing) < 1 by 0.000...1 (the needed knowledge about 0.000...1 is found in http://www.internationalskeptics.com/forums/showpost.php?p=10306748&postcount=4282).

jsfisher said:
ETA: Hint: "observe...from |R|".
Click to expand...
This is exactly the hint for you.
 
Last edited:
doronshadmi said:
You still exclude yourself as an essential factor of |R| observation of the real-line.

Without your |R| observation of the real-line, you simply unable to know why 0.999... (which is an |N| thing) < 1 by 0.000...1 (the needed knowledge about 0.000...1 is found in http://www.internationalskeptics.com/forums/showpost.php?p=10306748&postcount=4282).


This is exactly the hint for you.
Click to expand...

Awesome, Doron's age-old "I know what I am, but what are you? I am from rubber, you are from glue, anything you say bounces off me and sticks to you!" Kindergarten tactics.

If he does not answer I will start reporting those and the previous posts for breach of contract; he is not furthering the discussion; he just wants to win the fight.
 
realpaladin said:
Awesome, Doron's age-old "I know what I am, but what are you? I am from rubber, you are from glue, anything you say bounces off me and sticks to you!" Kindergarten tactics.

If he does not answer I will start reporting those and the previous posts for breach of contract; he is not furthering the discussion; he just wants to win the fight.
Click to expand...

There is no discussion coming from Doron because it is all like an LSD trip. There are colors like no colors anyone else has ever seen. He cannot describe things; none of it is real.
 
jsfisher said:
There is no discussion coming from Doron because it is all like an LSD trip. There are colors like no colors anyone else has ever seen. He cannot describe things; none of it is real.
Click to expand...

jsfisher, just observe the real-line from cardinality |R|.

If you do that, then and only then you will awake up from your only_|N| trip.

Simple as that.
 
Last edited:
Let's correct what I wrote in http://www.internationalskeptics.com/forums/showpost.php?p=10305716&postcount=4275.

The right one is this:

--------------------------------------

By using |R| size observation:

0.999...10 < 1 by 0.000...110

0.888...9 < 1 by 0.000...19

The difference between 0.000...110 and 0.000...19 is given by direct proportionality, according to the following formula:

abs( (1/9)/(1/10) ) (the result can't be expressed by any particular base, because this ratio is done between bases).

The general formula for all n>1 natural numbers is:

base j = 2 to n
base k = 2 to n

abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k.
 
Last edited:
doronshadmi said:
Let's correct what I wrote in http://www.internationalskeptics.com/forums/showpost.php?p=10305716&postcount=4275.

The right one is this:

--------------------------------------

By using |R| size observation:

0.999...10 < 1 by 0.000...110

0.888...9 < 1 by 0.000...19

The difference between 0.000...110 and 0.000...19 is given by direct proportionality, according to the following formula:

abs( (1/9)/(1/10) ) (the result can't be expressed by any particular base, because this ratio is done between bases).

The general formula for all n>1 natural numbers is:

base j = 2 to n
base k = 2 to n

abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k.
Click to expand...

And what is the use of this? Besides it being convoluted and based on the *WRONG*ful notion of there being a finite digit in an infinite series.

Also, this formula yields a rather weird result when j equals k... namely 1.

So the difference between two exact same numbers in the exact same base is 1?

If that is not proof of Doron's inability to do mathematics, then I do not know what more is needed.
 
The proportionality of a given value to itself is 1.

abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k calculates the value of proportionality within (0,1], such that a value < 1 means less self proportionality that can be translated into greater difference between two given values by the following formula:

n is some natural number > 1

base j = 2 to n
base k = 2 to n

1/abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k (the result can't be expressed by any particular base, because this ratio is done between bases).
 
Last edited:
doronshadmi said:
The proportionality of a given value to itself is 1.

abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k calculates the value of proportionality within (0,1], such that a value < 1 means less self proportionality that can be translated into greater difference between two given values by the following formula:

n is some natural number > 1

base j = 2 to n
base k = 2 to n

1/abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k (the result can't be expressed by any particular base, because this ratio is done between bases).
Click to expand...

Again, you are not supposed to be reading my posts; you are ignoring me. Keep this up and you'll be reported for categorically breaking the agreement.

Now, if you mean ratio, then do not use the word difference. Difference means the distance along a line that two values are apart.
Please be more rigorous in your use of language, it is so hobby-ish if you just 'do something'.

Furthermore, if the result can not be expressed in any particular base, then you can not define
doronshadmi said:
within (0,1], such that a value < 1 means less self proportionality that can be translated into greater difference between two given values by the following formula
Click to expand...

And again, you use the word difference where you want to use ratio.

Shoddy work that promises not much good for the rest of the dreamcastle that is being built on this...
 
Difference between values is not necessarily distance in terms of metric space.

For example, the different proportion between two values can be translated into greater values by the following formula:

n is some natural number > 1

base j = 2 to n
base k = 2 to n

1/abs( (1/(base j)) / (1/(base k)) ), such that j ≤ k (the result can't be expressed by any particular base, because this ratio is done between bases, so the formula itself is the result).
 
doronshadmi said:
By using |R| size observation:

0.999...10 < 1 by 0.000...110
Click to expand...
Simple counter example:

1/9 = 0.111...
2/9 = 0.222...
3/9 = 0.333...
...
9/9 = 0.999... = 1

Another approach:

9 * 1/9 = 9/9 = 1
9 * 0.111... = 0.999... = 1

Once more, with more rigor (I've tried to make each step as explicit and obvious as possible):

9repeatingequal1proof_zps2404921b.png


A similar proof exists for 0.888...9, as well as all other fixed point decimals. Every fixed point decimal in any base has an infinite decimal infinite decimal representation in that base:

0.1210 = 0.11999999...10
0.2510 = 0.2499999...10
0.3459 = 0.3448888888...9
100111.1101012 = 100111.1101001111111111...2
1.09 = 0.88888...9

To put it another way, every closed interval [n,m] has exactly zero length when n is fixed point decimal and m is it's infinite decimal expansion.

I know you have an intuitive belief that there must be some infinitesimal quanity between 0.999... and 1, but intuition is no substitute for a mathematical proof. How would you construct that quantity, and how do you show it is greater than 0? Can you show something more rigorous than an informal "size observation"?

The difference between 0.000...110 and 0.000...19 is given by direct proportionality, according to the following formula:

abs( (1/9)/(1/10) )
Click to expand...
This is not correct. The "proportionality" you mention is at best a statement about the rate of convergence between the sequences { 0.910 + 0.0910 + 0.00910 + ... } and { 0.89 + 0.089 + 0.089 +0.89 }, not their limit. They both converge to 1, implying 0.999...10 - 0.888...9 = 0.
 
Dessi said:
Simple counter example:

1/9 = 0.111...
2/9 = 0.222...
3/9 = 0.333...
...
9/9 = 0.999... = 1

Another approach:

9 * 1/9 = 9/9 = 1
9 * 0.111... = 0.999... = 1

Once more, with more rigor (I've tried to make each step as explicit and obvious as possible):

[qimg]http://i346.photobucket.com/albums/p412/julietrosenthal/9repeatingequal1proof_zps2404921b.png[/qimg]

A similar proof exists for 0.888...9, as well as all other fixed point decimals. Every fixed point decimal in any base has an infinite decimal infinite decimal representation in that base:

0.1210 = 0.11999999...10
0.2510 = 0.2499999...10
0.3459 = 0.3448888888...9
100111.1101012 = 100111.1101001111111111...2
1.09 = 0.88888...9

To put it another way, every closed interval [n,m] has exactly zero length when n is fixed point decimal and m is it's infinite decimal expansion.

I know you have an intuitive belief that there must be some infinitesimal quanity between 0.999... and 1, but intuition is no substitute for a mathematical proof. How would you construct that quantity, and how do you show it is greater than 0? Can you show something more rigorous than an informal "size observation"?


This is not correct. The "proportionality" you mention is at best a statement about the rate of convergence between the sequences { 0.910 + 0.0910 + 0.00910 + ... } and { 0.89 + 0.089 + 0.089 +0.89 }, not their limit. They both converge to 1, implying 0.999...10 - 0.888...9 = 0.
Click to expand...
Hey Dessi,

Your reply is right if you are using |N| observation of the real-line.

I use |R| observation of the real-line, as given in http://www.internationalskeptics.com/forums/showpost.php?p=10306748&postcount=4282, where the correction of the example there is given in http://www.internationalskeptics.com/forums/showpost.php?p=10324522&postcount=34.

Dessi said:
I know you have an intuitive belief that there must be some infinitesimal quanity between 0.999... and 1, but intuition is no substitute for a mathematical proof. How would you construct that quantity, and how do you show it is greater than 0? Can you show something more rigorous than an informal "size observation"?
Click to expand...
I use |N|<|R|, which is based on a rigorous mathematical proof.

------------------

Please also read very carefully all of what is written in http://www.internationalskeptics.com/forums/showpost.php?p=10316119&postcount=4298, http://www.internationalskeptics.com/forums/showpost.php?p=10318064&postcount=1 (some correction of this post: "X/4J)*4J, where j=1 to |N|" has to be "X/4J)*4J, where j=1 to |N|, such that |N| is not a value along the real-line") , http://www.internationalskeptics.com/forums/showpost.php?p=10318141&postcount=3 and http://www.internationalskeptics.com/forums/showpost.php?p=10318337&postcount=7, if you wish to reply to them.

Thank you.
 
Last edited:
Status
Not open for further replies.

Back
Top Bottom