how was NGC 3516 selected?
You are handwaving because that doesn't matter as far as my calculation is concerned. The calculation is independent of whether NGC 3516 was found or not. The calculation simply determines the probability of that particular configuration being found amongst the entire population of quasar/galaxies that we could observe assuming the mainstream's theories. And that probability is exceedingly small. So the fact that Arp found that case (and several others like it) after relatively few observations (compared to the total number of quasar/galaxy associations in a sky filled with literally billions of galaxies) should be a warning flag that something may be wrong with the mainstream's theories.
how many 'near NGC 3516 quasars' were known before Chu et al. planned their observations?
Again, that's handwaving because when the quasars were found doesn't affect the calculated probabilities in ANY way and because like or not there are 5 quasars with redshifts suspiciously close to Karlsson values aligned with the minor axis of NGC 3516 and no other objects identified as quasars in the observed field.
how are quasar redshifts distributed, in [0,3]? If they are not distributed equally (to within some bound), then probability calculations need to reflect that non-equal distribution.
I addressed that question. As I said, the frequency of redshifts is not constant over the entire range. Based on recent mainstream sources it looks like it rises from a finite value (about 1/8th of the max) near z=0 to a max at about z=1 to 1.5, then levels off till around z=2.5 to 3.0, where it precipitously drops reaching a value of only 1/40th to 1/50th the maximum at z=0.6. Thus, the low z data points (say below z = 1) are overweighted in my calculation compared to the higher z values in the range 1 to 3. That would affect the overall calculation more significantly if we observed that the separation between observed redshifts and Karlsson values as a percentage of their spacing between Karlsson values remained constant or trended upward or downward. But it doesn't. That spacing as a percentage goes up and down from point to point. Finding this effect is fairly involved but we can at least gage whether ignoring this in the calculation is conservative.
In the case of NGC 3516, observed z = 0.33, 0.69, 0.93, 1.40, 2.10. The Karlsson z = 0.3, 0.6, 0.96, 1.41, 1.96, 2.64. Therefore, the spacings are +0.03, +0.09, -0.03, -0.01, +0.14 which, as a percentage of the distance between the two nearest Karlsson values are 10%, 25%, 8%, 2%, 20%. Thus, the first two values with separations from the Karlsson value of 10% and 25% are overweighted, compared to the ones that have separations of 8%, 2% and 20%. That means in the calculation involving the three quasars with the lowest separations, the two lowest separations are underweighted compared to the highest separation of the three. Meaning that the corrected probability from that calculation
would be lower than was calculated. And in the two separate calculations to account for effect of the other two quasars, one of the two is somewhat overweighted but the other may be slightly underweighted. So I assert that incorporating this factor into this particular calculation would LOWER the final probability from the value I determined.
In looking this over for the NGC 5985 case, I find I made a mistake in the previous calculation. The observed z = 0.35, 0.59, 0.81, 1.97, 2.13. The spacings are therefore +0.05, -0.01, -0.15, +0.01, +0.17. In the previous calculation, I used a separation of +0.03 for the last data point instead of +0.17. That effects the calculation in a number of ways, so I'm going to redo the whole calculation before addressing the z distribution evenness issue.
Now we could do the same as before and simply calculate the combinatorial probability of finding the lowest three spacing data points, z= 0.35 (+0.05), 0.59 (-0.01) and 1.97 (+0.01). In that case, the required increment would be 0.10 and the probability would be 1/((30 * 29 * 28)/(3*2*1)) = 2 x 10
-4.
But that might significantly overestimate the probability since two of the data points are within an increment of only 0.02. So what's the combinatorial probability of finding 2 data points with a increment of 0.02? The answer is 1/((150 * 149 )/(2*1)) = 9 x 10
-5. Which is less than the above estimate so let's use it.
Now we add in the effect of the 0.35 (+0.05), 2.13 (+0.17) and 0.81 (-0.15) values. The probability of seeing the 0.35 data point with a increment of 0.10 is about 1/30 = 0.033; the probability of seeing the 0.81 data point with a increment of 0.30 is about 1/10 = 0.1; and the probability of seeing the 2.13 data point with an increment of 0.34 is about 1/8.8 = 0.11. Combined, these would reduce the 9 x 10
-5 probability estimate to only 3 x 10
-8.
Next, we must account for the actual number of quasars that might be seen near galaxies in groups of the size needed to do the above calculations. Previously, I found that the mainstream estimates there should be a total of about 410,000 quasars in the sky. And I then assumed (very conservatively, I think) that only half are near low redshift galaxies. That left us with 205,000 quasars to distribute. Then I assumed (again, very conservatively) that half of these would be distributed in quantities less than five to all the galaxies available, leaving 103,000 that are in groups of 5 near low redshift galaxies. Dividing by 5, the final result was 20,600 galaxies with at least 5 nearby quasars. Multiplying the above probability by 20,600 yields a probability of 5.4 x 10
-5.
It's at this point, however, that I notice another possible complication in my previous procedure. Since about half of the 3 x 10
-8 probability comes from only 2 quasars being together near a galaxy, the number of galaxies that might have 2 quasars is larger (by 2.5 times). Thus, the importance of those 2 quasars could be improperly diminished if I assume 20,600 as the total number of galaxies. Thus, we can expect an UPPER BOUND of 5/2 * 5.4 x 10
-5 = 0.000135 for the probability at this stage of the calculation. Let's conservatively use that.
Finally, we add in the fact that all 5 of these objects are aligned with the minor axis. As before, the alignment probability reduces the likelihood by 0.08, giving a final probability value of 0.000135 * 0.08 = 1.1 x 10
-5 for the NGC 5985 case.
(By the way, accounting for an increase in galaxy sample size in the NGC 3516 case because much of the probability only depends on 3 quasars, one can estimate an upper bound probability of 5/3 * 0.0005 (the original probability in that case) = 0.00083 ... a very, very small likelihood of that case turning up at all if we were somehow able to check every single quasar thought to be visible in the sky.
Now let's examine your concern about the z distribution in the NGC 5985 case. The percentage of distance between the two nearest Karlsson z values for the z = 0.35, 0.59, 0.81, 1.97, 2.13 observations are 16%, 3%, 42%, 1%, 25%, respectively. In this case, the 16%, 3% and 42% data points are overweighted, while the 1% and 25% data points are underweighted. In the two quasar calculation (which used z=0.59 and 1.97), the 3% value is somewhat overweighted. This would increase the probability at least a bit ... perhaps a factor of 2? But counteracting this is that fact that the z = 0.35 data point with a very large increment is underweighted. Likewise the z = 0.81 data point with an even bigger increment is also underweighted. But if you like, I'll still give you that factor of 2. In which case, the final probability of seeing NGC 5985, if one could check every single quasar out there, would only be 2 x 10
-5 ... again a VERY small number.
Any way you cut it, DeiRenDopa, this calculation proves that the mainstream's theory about quasars is on shaky ground. They need to reexamine that theory in light of this data or come up with an explanation why redshifts seem to be quantized around certain values and show up with a higher than expected frequency around galaxies along their minor axes. Or one has to illogically believe that Arp was REALLY LUCKY in turning up 2 cases with likelihoods of only 0.0008 and 0.0002 even if all the galaxies in the sky with quasars could be examined (which he didn't come close to doing).
your calculation, on its own, would seem to apply to any set of three numbers in [0,3]
No, the three numbers that turned up aren't just any three numbers, are they. They are all close to values that were determined without any reference to the data in these particular samples. Or so I believe.

As I noted earlier, if the range is [0,3], then all the Karlsson values in that range need to be included.
And as I noted in my response, there is nothing in the theory that requires quasars be at all the Karlsson values around any given galaxy at any one time.
Beachooser wrote:
Here's a 2005 study
http://www.iop.org/EJ/abstract/1538-3881/129/5/204 that indicates an average density of 8.25 deg-2 based on the SDSS survey then argues it should be corrected upward to 10.2 deg
-2 to make it complete. And if you go to the SDSS website (
http://www.sdss.jhu.edu/ ) you find they say the effort will observe 100,000 quasars over a 10,000 deg2 area. That also works out to about 10 quasars deg-2. So it looks like I used a number that was 3 times too large in my earlier calculation. In this revised calculation, I will only assume the average quasar density is 10 deg-2. That means the total number of quasars than can be seen from earth is around 410,000.
The Chu et al. paper carefully explains how they chose which objects to observe (in order to measure redshifts); the "average density" of quasars you need to use in this part of your calculation is that which would be obtained if the search method used in Chu et al. were to be used over the whole sky. As there appears to be no effort to explain this, in any quantitative fashion, let alone estimate it, you are left with an unknown.
Let me emphasize that my calculation actually has nothing to do with the Chu et. al. paper. If you don't like the "average density" of quasars that I used for all the quasars in the sky (i.e., 10/deg
2), then I'll make you the same offer I made to David. You provide that number and we will just insert it in the calculation and see what we get. I used 10/deg2 because the SDSS study and website says that's the average density. It's why they indicate there are in total about 400,000 quasars in the visible universe. If you want me to use whatever Chu claimed is the average density over the ENTIRE sky, then just tell us what Chu says that is. But be prepared to justify it, if it happens to disagree with the SDSS estimate. After all, the SDSS estimate is based on the most complete study of quasars that is available (you folks kept telling me that) and papers have been published by mainstream astronomers that in fact conclude the SDSS study is very close to complete in it's identification of the quasars that are out there in the section of the sky that was surveyed). If you don't like the assumption that the density of quasars in the quarter of the sky that was surveyed is the same as the density in the three-quarters that was not surveyed ... take it up with the SDSS authors. :)
Frankly, I think you are just doing more hand-waving ... now desperate to avoid accepting what is a rather obvious conclusion for this set of calculations. :D
you need at least a measure of the variation in average density (as well as the average density), to make the sorts of estimates this part of calculation aims to do.
No, I don't. The results of my calculation are not affected by the fact that more quasars might be located in one little area of the sky than in another, as long as the average density of the entire sky is 10/deg2. The total number of galaxies with 5 or more quasars (or 2 or 3 in the later calculations) near them will remain the same. Somehow, I think you aren't conceptualizing the true nature of this calculation.
BeAChooser wrote:
But the truth is that most quasars do not lie close to galaxies at all (certainly not galaxies where we can discern any detail as is the case in all three examples of interest here) so that's why I later multiplied the calculated probability by 0.10 to account for the assumption that only 10% of quasars lie next to a galaxy. I still think that's probably a reasonable number. But for this calculation, I'm going to give your side the benefit of the doubt and assume that fully half of all quasars are near galaxies. That has to be very conservative. Wouldn't you agree. So now there are 205,000 in the population that we need to distribute amongst galaxies.
Making up numbers, and using one's intuition about what's conservative, reasonable, etc, in astronomy is an almost certain way to be wrong.
Do you honestly think that more than half of quasars lie near low redshift galaxies? Care to prove that? Do you have ANY basis for thinking that? The fact that Arp could only come up with a limited number of anomalous associations, after studying what must have been thousands of cases, seems proof enough that more than half of quasars must not be near low redshift galaxies from our viewing perspective.
But I tell you what, if you have evidence that the percentage is higher than 0.5, then just offer it. Don't be coy. We can factor that into the calculation of probabilities and see what happens. :)
Or maybe there's another way we can come up with an estimate of the number of galaxies we need to consider as being near quasars. What we need to know is the number of galaxies that are low redshift ... say within a redshift of about 0.01 (since both of the cases in my calculation have redshifts less than that value).
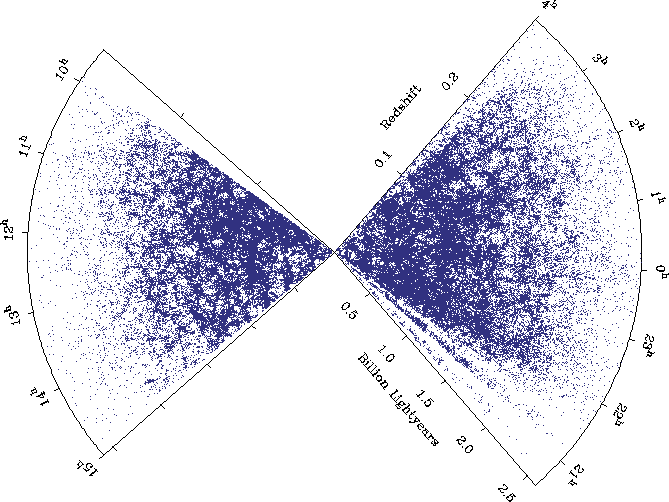
This
shows galaxies versus redshift in the 2dF survey. According to the NASA APOD text, there are about 200,000 galaxies in that sample. According to this; http://www.mso.anu.edu.au/2dFGRS/ , the area surveyed was approximately 1500 deg2.
Now looking at that plot, I visually estimate that the density is roughly constant out to a z of about 0.15 . The percent area that the z=0.01 zone occupies in the z=0.15 region is PI * (0.01/0.15)2 = .014. Probably a third again as many galaxies lie outside the z=0.15 region in that image. So the number of galaxies within z=0.01 is probably no more than 1 percent of 200,000. So within a 1500 deg2 surface, there would be .01*200,000 = ~ 2000 galaxies. Which means there are about 1-2 galaxies per square degree. According to one source I found, most of the galaxies in near-field surveys are smaller than 30 - 40 arcsec, meaning they occupy only a small fraction of any given square degree field (because one arcsec is 1/3600 of a degree). Another source noted that even in galaxy groups, the distance between member galaxies is typically 3-5 times the diameter of the galaxies. Even the giant Whirlpool galaxy, which was the first to show a spiral form, only has an apparent diameter of 10 arcmin. Even the naked eye Andromeda galaxy, M31, our nearest neighbor only has an apparent diameter of 180 arcmin in it's largest dimension. NGC 3516 has a apparent diameter of only a few arcmin. So with only 10 quasars per square degree of sky on average, it would seem there would be plenty of room for quasars that are not associated with local, low redshift galaxies. Or do you wish to contest this further? :)
Earlier you introduced a paper by L-C&G, which presented some rather concrete numbers of just what you are trying to estimate; why not use what's in that paper?
Are you saying I should use their estimate for the average quasar density per square degree of sky? Or their estimate of what fraction of the quasars are actually within a degree of galaxies? Or their estimate of what fraction are in quasar/galaxy associations with 5 quasars per galaxy? Did they actually estimate any of those numbers? I don't recall seeing it in the paper. If you see those numbers, please point them out to me.