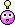"...where Distinction is a first-order property."
This phrase continues to appear with great regularity in the stuff we have seen of your work. So far, we don't have a satisfactory explanation of what the phrase means. Perhaps you can provide one, MosheKlein.
What do you mean by the word,
distinction? Your word choice suggests it should have something to do with the word,
distinct, in English, but then it would have to be relative to something else, not a property of a single thing. A is distinct from B.
What aspect makes it
first-order? I hope you realize
first-order has a specific mathematical meaning having to do with predicates and quantification, so I am curious how
distinction (whatever that really means) takes on first-order characteristics.
By the way, MosheKlein, there is something you should know. Your Organic Mathematics concepts may be crystal clear to you, but they are very poorly expressed in your writings. People here in this Forum can be a great resource for moving your ideas into legitimate mathematical expression. We'd very much like to help, but first we need to understand what it is your are trying to say.
If you react positively to the help provided here, people will react very positively to you. If, instead, to blame everyone else, as Doron has been doing, for any communication problems, don't expect people to be always friendly.

 to the forum.
to the forum.