Clear evidence that 9/11 was an inside job
- Thread starter FatFreddy88
- Start date
The Pig
Thinker
- Joined
- May 16, 2006
- Messages
- 171
Is the flight-path in the Google Earth image here inaccurate? This is what we've been working from? I smell the beginnings of a 'Too Big To Be A 757' CT (TBTBA757©).
We didn't get up to the fish-eye lens considerations - we're still not past trig 101.
BCR
Master Poster
- Joined
- Dec 6, 2008
- Messages
- 2,278
No, GE is just fine. Perpendicular to the image plane takes you to a point inside the Pentagon and corresponds with the gatehouse. The gatehouse is oriented 64 degrees from N. The aircraft is almost parallel with the image plane of the camera. So the distance from the camera to the front of the aircraft, and the distance from the camera to the tail of the aircraft are not going to be that much different. Keep in mind you are not dealing with a right triangle. The triangle of interest is from the camera to the front of the aircraft, to the rear of the aircraft, and the length of the aircraft. You could approach it as the difference between two right triangles, but the right angle would be the same for both triangles corresponding with the intersection of the flight path and the line perpendicular to the camera plane.
More:
Of course keep in mind that the 'difference in two right triangles' would only be an approximation since there is a 2 degree difference between the camera plane and aircraft heading.
Update 2:
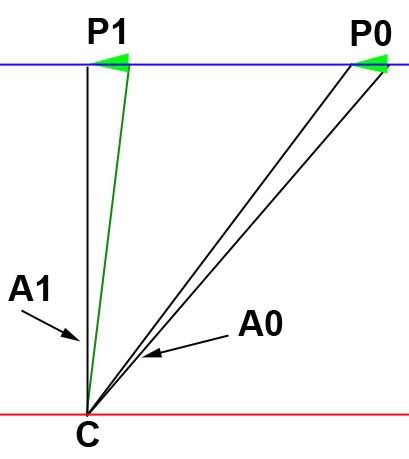
Perhaps this will make it clearer. Angle A0 will definitely be a little smaller than if the aircraft was directly in front of the camera, angle A1 (perpendicular to the image plane). Now you can solve using the difference between two right triangles to find A0 for an approximation. But, since the aircraft heading is 2 degrees less than the camera plane you are actually dealing with an obtuse triangle even at position P1 instead of a right triangle. It is the angular difference you are looking for in this case (measured in mm with a ruler on computer screen instead of degrees).
Here is the equation you need to solve for the angle:
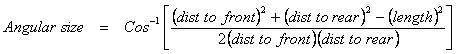
Now FatFreddy88, solve the equation for P0 and P1 and you'll have your answer. However, I can tell you right now that you cannot measure precise enough with your silly ruler to get there.
Last edited:
Oystein
Penultimate Amazing
- Joined
- Dec 9, 2009
- Messages
- 18,903
This is getting silly now, but I must insist...
In your post 228, you talked about two lines in my image:
We talked about D-B (62mm) and D-C (47mm). D-C is NOT in a way "marked" along D-B; there are two wholly different lines. You said "the difference is roughly 24%", and I pointed out that the difference could just as well be said to be roughly 32%. Just depending on which length is your 100%
FALSE! I did not maintain that at all! We never got to that point, because you failed to draw an image to explain what you measure! (And because I think you set out to measure lengths whose location you can't determine in the photo. You started out on the wrong foot).
No-one here can "agree" with me on this, because I didn't say that.
Oystein
Penultimate Amazing
- Joined
- Dec 9, 2009
- Messages
- 18,903
Yes.
He referred to my image:
and for reasons unbeknownst to any mortal soul, he measured the lengths of D-B (from center of plane to impact point) and D-C (plane to the perpendicular projection of center of plane on Pentagon wall) and decided that the difference between the two lengths was 24%. I don't recall what he needed that for, it makes absolutely no geometrical sense, since only the relatrive distances from camera (A) could be helpful in determining apparent size, but before he went on, I pointed out that the difference could just as well be said to be 32%. Then we got stuck on that detail, and never got out of the mess again; it was for me just a token to show how Freddy is struggling with simple math.
Oystein
Penultimate Amazing
- Joined
- Dec 9, 2009
- Messages
- 18,903
Thanks, BCR, that post is helpful in three different ways:
A) You show a result using a completely different (and valid) method (2D rendering from 3D model), and it is immediately apparent to even a total math ignoramus what the result is.
One might critcize that the method is not transparent, one has to believe that everything was done correctly, or use the same software, which is, for now, beyond my or Freddy's capabilities.
B) You point out lens distortion, which I didn't think of so far, and that is an entirely valid point. In case Freddy doesn't get it: A feature in the center of the photo might appear larger or smaller if you pan the camera without changing its location. Which is why we can't compare the apparent length of the plane (off to the right) to the height of the building (closer to center of photo).
There are other distortions that we also did not take into account yet; for example, using a simple sinus function, or cross-multiplication on similar triangles, to compute the apparent shortening of the plane due to distance and angle, implicitly assumes parallel projection, or infinite camera distance. We'd e more precise if we talked about angles with camera position as vertex.
However, my work is still a good refutation of FatFreddy's assertion, for I showed that even using his invalid or imprecise method, the formally correct result is that the plane fits behind the box. In other words: Freddy used an invalid method, and made errors within that method.
C) On the 2D rendering of the sight from camera, I noticed for the first time that the heli tower / firehouse obscures the far wing of the Pentagon face. I suspect Freddy, too, hasn't noticed that we can't see (and measure) any part of the wall beyond the protruding center portion.
In sum, Freddy's work has now been destroyed in several different ways. Let's see how he'll take it.
Erock
Muse
He does this on every forum, then comes back later when the dust has settled and offers the identical argument. I cannot fathom that kind of mentality, he constantly puts himself out as a twoofer, but shows anything but.
He sees responses as some kind of triumph
http://www.spurstalk.com/forums/showpost.php?p=5257311&postcount=2350
from this page:
http://www.spurstalk.com/forums/showthread.php?t=144487&page=91
To anyone who has some confusion about this issue, there have been some extremely well formulated posts in this thread which to anyone with rationale explains it perfectly.
aggle-rithm
Ardent Formulist
BCR
Master Poster
- Joined
- Dec 6, 2008
- Messages
- 2,278
But it is transparent. This is from Mike Wilson's work with the engineering-grade software Solidworks. He has made his models available for anyone to download and verify. A number of people in this thread have done so, even pointing out the one error he did make, the height of the Pentagon (which does not impact the results under discussion).
Just because something (like math) is beyond Freddy's capabilities does not negate its value. He likes to make links to CIT stuff, and I already mentioned that the French guy who did the 3D work for their first Pentacon production replicated the lens and scene using an entirely different software package with the same results (unfortunately, CIT drove him crazy and he deserted ship). I did the same thing with Maya years ago (but I'm no artist and mine are not pretty enough for public view). He also likes to link P4T. I'm the one who introduced CPT Bob to Maya years ago and sent him a copy of the video and learning CD's. *They needed someone to replace Pierre. However, unlike Mike Wilson who makes his work public for replication by others, CPT Bob does not (so who is the 'truth-seeker'?)
Last edited:
The Pig
Thinker
- Joined
- May 16, 2006
- Messages
- 171
BCR, assuming you haven't lost the will to live already; my rough... actually very rough extrapolations from GE show:
* The flight-path (BD in the above image we've been working from) as approximately 53 or 233 degrees from North.
* The line-of-sight (AD in the above image) from the camera to the plane's centre as approximately 21 or 201 degrees from North.
I accept the plane may have been oriented 62 degrees from North, but I still can't reconcile the 2% difference you talked about (although this may well be me being t'ick).
The maths in my earlier post may well be flawed (I'll look at this once I grasp the 2%); the reason I chimed in on this thread was FF88's spurious method for working out the effective foreshortening of the plane.
* The flight-path (BD in the above image we've been working from) as approximately 53 or 233 degrees from North.
* The line-of-sight (AD in the above image) from the camera to the plane's centre as approximately 21 or 201 degrees from North.
I accept the plane may have been oriented 62 degrees from North, but I still can't reconcile the 2% difference you talked about (although this may well be me being t'ick).
The maths in my earlier post may well be flawed (I'll look at this once I grasp the 2%); the reason I chimed in on this thread was FF88's spurious method for working out the effective foreshortening of the plane.
BCR
Master Poster
- Joined
- Dec 6, 2008
- Messages
- 2,278
No, my approach was from a completely different starting point since I have no idea of what the guy is talking about. I was addressing his cock-a-mamy measuring something on his computer screen and calling it evidence of anything (except maybe the need to clean it).
My exercise was simply to show the guy that what he is actually measuring is angular size. In this case, the aircraft is flying parallel (approximately) to the image plane, and the 2 degree difference is just not going to be a significant factor. What is going to be a factor is the angular distance from the line normal to the camera plane. In this case, there is also angular distortion from the lens to consider.
Since I had no darn clue what his stupid C-D, D-C (or whatever) had to do with anything, I thought I would address his root argument. Darn, even the units of measure he is using (mm) don't apply .... convert it to radians or degrees, minutes, seconds so that we are all on the same page Freddy. The Meter is a measure of length, not angular size. You are submitting a measured length of two points on your computer screen which makes absolutely no sense at all in the real world.
BCR
Master Poster
- Joined
- Dec 6, 2008
- Messages
- 2,278
Yes, and that is to whom my comments are directed at. I have not gone over your stuff. Freddy wants me to comment on who I agree with, you or him. Before I can do that, he has got to show me his argument. I'm not going to waste time going over yours or anyone else's math to see who is right or wrong unless he gives me his mathematical arguments with which to compare them with. So far, all I've heard from him are stupid measurements of his computer screen with a ruler.
Last edited:
Dave Rogers
Bandaged ice that stampedes inexpensively through
BCR
Master Poster
- Joined
- Dec 6, 2008
- Messages
- 2,278
So that we are on the same page, I added my reference points to your image.
I think you can see how they correspond a little better. The 2 degrees I was talking about is the difference between the camera plane and the aircraft's path.
I Am The Scum
Philosopher
- Joined
- Mar 5, 2010
- Messages
- 5,787
I think what you're failing to understand is that percentages are not, in and of themselves, actual quantities. By their nature, percentages must relate to two quantities to have meaning. You can't just say X is 32%. The question one must ask to evaluate that point is, "32% of what?"
Say I go to the store to buy a gallon of milk for $2 (it's on sale). I get to the store to realize I have only $1 in my pocket. The difference between these two numbers is not 100% or 50%, or any percent. The difference is one dollar. However, we can compare the two numbers, in two different ways. We could say that my cash is 50% of the price. Or, we could say that the price is 100% more than my cash. We're comparing two quantities in specific ways.
The Pig
Thinker
- Joined
- May 16, 2006
- Messages
- 171
Ahhh. Thanks for the reply, I see where the 2% comes in now. In other words, the difference between the camera-plain (the centre of shot) and the perpendicular to the flight-path is about 2%.
I don't think the camera-plain is so important in this case; we need to look at direction of the line-of-sight between the camera and the centre of the plane. My rationale:
* I take an object that is 50m x 3m x 0.01m to the Pentagon, and place it 250m away from the camera, and at the very edge of its field-of-vision.
* (A) I first orientate it so that it is aligned with the camera's line-of-sight.
* (B) I then orientate it so that it is aligned with the camera plain.
* We would see more of the object in instance B (it would be near invisible in instance A).
Even if the plane was perpendicular to the camera-plain, because it was way to the right of shot, it would have appeared longer had it been perpendicular to the line-of-sight between the camera and the plane. The ratio between apparent and actual length was what I was trying to work out.