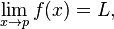Deeper than primes

jsfisher · Sep 3, 2011

doronshadmi said:
'rigorous' is not less than the complementary understanding of non-locality and locality as a one unified framework.

It means that visual_spatial AND verbal_symbolic skills are actually used.

A common misunderstanding of what is written above, is based on the equivalence between 'rigorous', 'strictness', or 'step-by-step' reasoning, because only verbal_symbolic skills are used.

When I asked if you knew what the word, rigorous, meant, a simple "No" would have sufficed.

doronshadmi said:
Here is an example of how 'rigour' is based only on verbal_symbolic skills ( http://oregonstate.edu/instruct/mth251/cq/Stage3/Lesson/theDefinition.html ) actually does not work, exactly because by using visual_spatial AND verbal_symbolic skills epsilon > delta > 0.

Ah, Doron. I see you are back trying to disprove definitions again. The URL provides a perfectly fine definition for a certain type of limit.

Oh, and by the way, no where is it required that epsilon > delta as you claim, unless, of course, you were trying to point out yet again that when you introduce your visual/spatial skills, you get the wrong result.

doronshadmi · Sep 3, 2011

jsfisher said:
When I asked if you knew what the word, rigorous, meant, a simple "No" would have sufficed.

"No" is a sufficient answer only to closed systems like you that can't get http://www.internationalskeptics.com/forums/showpost.php?p=7535018&postcount=16319.

jsfisher said:
The URL provides a perfectly fine definition for a certain type of limit.

no where is it required that epsilon > delta as you claim,

This URL does not provide any "perfectly fine definition for a certain type of limit".

( http://oregonstate.edu/instruct/mth251/cq/Stage3/Lesson/theDefinition.html )

The lim f(x) = L x --> a if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta.

Since |f(x) - L| > 0 and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false.

This simple fact is easily understood by using visual_spatial AND verbal_symbolic skills.

"if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta" is based only on verbal_symbolic skills and therefore it does not hold water.

jsfisher · Sep 3, 2011

doronshadmi said:
It does not matter

It does matter. It shows yet again how muddled your thinking is. You grossly misunderstand things then gloss over details to protect your ignorance.

both epsilon and delta > 0

Yes, that's how the definition reads, but not epsilon > delta as you alleged.

so this URL does not provide any "perfectly fine definition for a certain type of limit".

In what way is it deficient? Just because you may not like the definition, doesn't make it lacking. Mathematics is not obligated to get your approval for its terminology.

If it is deficient as a definition, surely you can provide a simple example where it comes up short.

doronshadmi · Sep 3, 2011

jsfisher said:
It does matter.

Yes, that's how the definition reads, but not epsilon > delta as you alleged

Again, it does not matter. What matters is that both epsilon and delta > 0.

jsfisher said:
no where is it required that epsilon > delta as you claim,

You are missing the important things (where my mistake about "epsilon > delta" does not change it (the right one is: "epsilon > 0 and delta > 0")).

This URL does not provide any "perfectly fine definition for a certain type of limit".

jsfisher said:
In what way is it deficient? Just because you may not like the definition, doesn't make it lacking. Mathematics is not obligated to get your approval for its terminology.

If it is deficient as a definition, surely you can provide a simple example where it comes up short.

( http://oregonstate.edu/instruct/mth251/cq/Stage3/Lesson/theDefinition.html )

The lim f(x) = L x --> a if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta.

Since |f(x) - L| > 0 and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false.

This simple fact is easily understood by using visual_spatial AND verbal_symbolic skills.

"if and only if for every epsilon > 0 there is a corresponding delta > 0 such that |f(x) - L| < epsilon
for all x with 0 < |x - a| < delta" is based only on verbal_symbolic skills that do not hold water, because by using these partial skills one can't understand that there is no homeomorphism between 0 dimensional space and 1 dimensional space.

jsfisher said:
It shows yet again how muddled your thinking is. You grossly misunderstand things then gloss over details to protect your ignorance.

Well, I made a mistake about "epsilon > delta" (the right one is: "epsilon > 0 and delta > 0").

This mistake does not change the fact that your verbal_symbolic_only reasoning can't comprehend that since |f(x) - L| > 0 and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false, no matter what verbal_symbolic string follows it.

jsfisher · Sep 3, 2011

doronshadmi said:
This URL does not provide any "perfectly fine definition for a certain type of limit".
...
Since |f(x) - L| > 0

You made that part up. There is no such constraint in the definition.

...and |x - a| > 0 because there is no homeomorphism between 0 dimensional space and 1 dimensional space,
the expression "f(x) = L x --> a" is false.

Again, you are trying to disprove a definition. Do you not know what a definition is?

In this particular case, the meaning of "the limit of f(x) = L as x approaches a" is being defined. That stuff between the quotes isn't true or false; it is the subject of the definition.

Definitions in Mathematics are not subject to your disapproval nor can the fall victim to disproof.

doronshadmi · Sep 3, 2011

jsfisher said:
You made that part up. There is no such constraint in the definition.

I know.

In order to understand that |f(x) - L| > 0 you have to use at least your visual_spatial AND verbal_symbolic skills.

Without actually doing it (which enables you to know that there is no homeomorphism between 0 dimensional space and 1 dimensional space) you can't get that the expression "f(x) = L x --> a" is false.

jsfisher said:
Again, you are trying to disprove a definition. Do you not know what a definition is?

It is a valid mathematical expression that is based at least on one's visual_spatial AND verbal_symbolic skills.

jsfisher said:
In this particular case, the meaning of "the limit of f(x) = L as x approaches a" is being defined. That stuff between the quotes isn't true or false; it is the subject of the definition.

Definitions in Mathematics are not subject to your disapproval nor can the fall victim to disproof.

"the limit of f(x) = L as x approaches a" is a false stuff.

The true stuff is "f(x) ≠ L as x approaches a" and this true stuff is known if visual_spatial AND verbal_symbolic skills are used.

jsfisher · Sep 3, 2011

Ok, then. Definitions are inadmissible in Doronetics. Nothing is defined.

Can't be every useful, then.

jsfisher · Sep 3, 2011

doronshadmi said:
jsfisher said:

You made that part up. There is no such constraint in the definition.

Click to expand...

I know

Interesting. You know it is just something you made up, but to proceed with it anyway.

In order to understand that |f(x) - L| > 0 you have to use at least your visual_spatial AND verbal_symbolic skills.

You mean your very special visual/spatial skills. The rest of us don't have your unique talent to disprove definitions by arguing against things that aren't even there.

doronshadmi · Sep 3, 2011

jsfisher said:
Ok, then. Definitions are inadmissible in Doronetics. Nothing is defined.

Can't be every useful, then.

A typical reply of a limited mind that is based only on verbal_symbolic skills.

doronshadmi · Sep 3, 2011

jsfisher said:
Interesting. You know it is just something you made up, but to proceed with it anyway.

The "I know" means that I know that you can't get what I say (you say: "There is no such constraint in the definition") because you are using only your verbal_symbolic skills.

This time please read the whole first part of http://www.internationalskeptics.com/forums/showpost.php?p=7536466&postcount=16326 in order to understand the "I know".

jsfisher said:
You mean your very special visual/spatial skills. The rest of us don't have your unique talent to disprove definitions by arguing against things that aren't even there.

Again, I know that your verbal_symbolic-only skills are insignificant in order to get that the expression "f(x) = L x --> a" is false.

Once again http://www.internationalskeptics.com/forums/showpost.php?p=7535018&postcount=16319.

jsfisher · Sep 3, 2011

doronshadmi said:
The "I know" means that I know that you can't get what I say (you say: "There is no such constraint in the definition") because you are using only your verbal_symbolic skills.

You continue to accuse others of your own unique failings.

This time please read the whole first part of http://www.internationalskeptics.com/forums/showpost.php?p=7536466&postcount=16326 in order to understand the "I know".

Have you finally stopped revising it?

Again, I know that your verbal_symbolic-only skills are insignificant in order to get that the expression "f(x) = L x --> a" is false.

You never understood limits. We get that. That doesn't stop us from defining what we mean by an expression involving limits. If "X means Y", then I would have expected only a mentally deficient person to rant that it is not rigorous because X is false. I don't think you are mentally deficient, just a crank, but you are certainly having trouble with the whole definition concept.

doronshadmi · Sep 4, 2011

jsfisher said:
I don't think ...

Well, you are using partial thinking, the verbal_symbolic_only one.

This partial thinking can't actually deal with the discussed subjects, where Limit is one of them (and more generally, it can't get the actuality of Definition that is based on Visual_spatial AND Verbal_symbolic reasoning).

jsfisher said:
You never understood limits.

Wrong, your verbal_symbolic_only reasoning can't get the following valid expression "f(x) ≠ L if x only approaches (= can't actually reach) a".

Visual_spatial AND Verbal_symbolic reasoning naturally get that "f(x) ≠ L if x only approaches (= can't actually reach) a".

Some hint: There is no homeomorphism between 0 dimensional space and 1 dimensional space.

jsfisher · Sep 4, 2011

doronshadmi said:
Wrong, your verbal_symbolic_only reasoning can't get the following valid expression "f(x) ≠ L if x only approaches (= can't actually reach) a".

First off, it is not "f(x) = L as x approaches a". Learn to read. It is "the limit of f(x) = L as x approaches a".

Second off, "approaches" does not mean "can't actually reach". Learn the meanings of words.

Third off, the whole thing is a definition. Learn to comprehend.

And as for our silly repeated gibberish about what an arbitrary function can and cannot do, consider the trivial example where f(x) = 2. Not a very interesting function, but a function nonetheless. Let L = 2, then f(x) = L as x approaches anything and everything within the domain of f().

doronshadmi · Sep 4, 2011

jsfisher said:
First off, it is not "f(x) = L as x approaches a". Learn to read. It is "the limit of f(x) = L as x approaches a".

Learn to understand instead of playing with symbols.

x is local w.r.t the domain of f(), where the domain of f() is non-local w.r.t x.

For example: x is equivalent to n dimensional space, where the domain of f() is equivalent to n+1 dimensional space.

Since there is no homeomorphism between n dimensional space and n+1 dimensional space, the expression "L ≠ the limit of f(x) as x approaches a" is true.

jsfisher said:
Second off, "approaches" does not mean "can't actually reach". Learn the meanings of words.

"approaches" is "no more than getting closer to".

In order to "actually reach" a, x must be closest w.r.t a, such that x is actually a.

Since there is no homeomorphism between n dimensional space and n+1 dimensional space, x is "no more than getting closer to" a.

jsfisher said:
Third off, the whole thing is a definition. Learn to comprehend.

Call it whatever you like, the expression "L = the limit of f(x) as x approaches a" is a false expression.

jsfisher said:
Let L = 2, then f(x) = L as x approaches anything and everything within the domain of f().

Again, "approaches" is "no more than getting closer to" so "x approaches anything and everything within the domain of f()" means that "f(x) ≠ L".

-----------------

jsfisher, once again it is shown how your verbal_symbolic_only skills simply can't comprehend the difference between "approaches" and "actually reach", exactly because your visual_spatial skills are not used.

Once again it is shown that, for example, http://www.internationalskeptics.com/forums/showpost.php?p=7511706&postcount=16304 is beyond your mind.

jsfisher · Sep 4, 2011

I write this:

jsfisher said:
First off, it is not "f(x) = L as x approaches a". Learn to read. It is "the limit of f(x) = L as x approaches a".

and you reply with this:

doronshadmi said:
Learn to understand instead of playing with symbols.

x is local w.r.t the domain of f(), where the domain of f() is non-local w.r.t x.

For example: x is equivalent to n dimensional space, where the domain of f() is equivalent to n+1 dimensional space.

That is about as non-responsive as one can get. Doron, seriously, work on the reading comprehension.

Since there is no homeomorphism between n dimensional space and n+1 dimensional space, the expression "L ≠ the limit of f(x) as x approaches a" is true.

Hmm, now how could we possibly evaluate the merits of Doron's claim? Oh, I know, we'd need to refer to the definition of limit....

jsfisher said:
jsfisher said:

Second off, "approaches" does not mean "can't actually reach". Learn the meanings of words.

Click to expand...

"approaches" is "no more than getting closer to".

In order to "actually reach" a, x must be closest w.r.t a, such that x is actually a.

Again, learn the meaning of words. "I approach the door" does not mean "I can't reach the door." The sloppy mistakes you continue to make, Doron, are a symptom of true crank.

jsfisher said:
jsfisher said:

Third off, the whole thing is a definition. Learn to comprehend.

Click to expand...

Call it whatever you like, the expression "L = the limit of f(x) as x approaches a" is a false expression.

Again, the only way to establish that would be to use the definition of limit. You continue to leap over that part so you can maintain your dislike for and misunderstanding of such a basic concept.

jsfisher said:
jsfisher said:

Let L = 2 [and f(x) = 2], then f(x) = L as x approaches anything and everything within the domain of f().

Click to expand...

Again, "approaches" is "no more than getting closer to" so "x approaches anything and everything within the domain of f()" means that "f(x) ≠ L".

Excellent. According to Doron, if f(x) = 2, then f(x) ≠ 2.

You have exceeded yourself, Doron. Well done!

The Man · Sep 5, 2011

doronshadmi said:
Indeed duality always involves both, such that it is changeable from 50%;50% which-way state (which is characterized by a wave pattern with non-strict localization) to 0%;100% which-way state (which is characterized by a single slit pattern with strict localization) by using partial measurements that are done between 50%;50% to 0%;100% , as shown, for example, in http://www.askamathematician.com/2011/06/q-what-is-a-measurement-in-quantum-mechanics/:

Doron, a single photon in impacts only a single spot on the screen. The distribution patterns you refer to are exactly that, the patterns of multiple photon impacts that are distributed over the screen. So now by your own assertions both your “non-strict localization” and “strict localization” are just distribution patterns. Would a single photon impact on the screen be a “strict localization” or a “non-strict localization”?

doronshadmi said:
Dr. Shahar Dolev wrote:

I'll translate it:

"במאמר מפתח הראה אנגלרט⁵⁸ כי ניתן לגרום למערכת קוונטית לבטא את כל ספקטרום ההתנהגות שבין גל לחלקיק"

"In a Key article Englert⁵⁸ showed that it is possible to cause a quantum system to express the whole spectrum between a wave and a particle."

It does not mean that this sanctum is not a complementary state between a wave and a particle.

By using URDT one enables to measure this spectrum, which exists between the non-locality of a wave state and the locality of the particle state.

Fine then show exactly how you “measure this spectrum” with your TURD, or stop lying.

doronshadmi said:
The non-locality is expressed as superposition of identities of the quantum objects, which has the symmetrical nature of wave patterns.

A gradual break of this symmetry provides the strict local nature of quantum objects as particles.

Both the 50/50 and 0/100 distribution pattern examples in the link you cited are symmetrical (though about different axis). Please learn something (like what symmetrical means).

It that your problem that you just want to conflate symmetry breaking in your nonsense somewhere?

doronshadmi said:

Tools like Schrödinger equation are not useful in this case because they are based on strict variables that prevent the ability to deal with the superposition of identities of the quantum objects.

Click to expand...

The Schrödinger equation claims no such basis, stop lying Doron.

And while you’re at it read your own cited references.

The Copenhagen interpretation of quantum mechanics (which comes in a couple different flavors) is generally stated as “a thing is in a super-position of states until it’s measured”. Some people (including very few physicists) have come to the conclusion that “measurement” means “measured by something conscious, and also we’re all part of the same energy field, so we’re psychic, and modern science is only now coming to understand what eastern philosophers have known for millennia”.

Just to be clear, the Copenhagen interpretation is a bottomless font of problems and paradoxes, of which the “measurement problem” is one of the more interesting (but still: one of many). Luckily, since Copenhagen is based on an assumption (“things are in many states until measured”) that never needed to be made, isn’t well-defined, and is in no way supported by any kind of evidence, it can be abandoned giving rise to the Many Worlds Interpretation. Sorrowfully, it’s often found unabandoned (particularly in new age literature).

Click to expand...

He is specifically asserting the notion you cling to and so readily misrepresent (“things are in many states until measured”) should be abandoned. How’s that coming for you?

doronshadmi said:

Again "A,B"-only reasoning can't comprehend, for example, http://www.internationalskeptics.com/forums/showpost.php?p=7511706&postcount=16304 .

Click to expand...

Again stop simply trying to posit aspects of your own failed reasoning onto others and indicate that specific “transition” in your TURD, as asked before.

doronshadmi said:

You can't because you are closed under it.

Click to expand...

The Man said:

It is just your nonsense Doron. Please show how you use it to solve anything.

Click to expand...

doronshadmi said:

First please get out of your strict-only box. Without actually doing it, you can't get URDT.

Click to expand...

It is your “strict-only box”, simply trying to posit it onto others will not help you. You claimed a distinction with your TURD so you show that distinction with your TURD.

doronshadmi · Sep 5, 2011

jsfisher said:
I write this:

and you reply with this:

That is about as non-responsive as one can get. Doron, seriously, work on the reading comprehension.

jsfisher, seriously, work on getting out of your verbal_symbolic_only skills, by simply use your visual_spatial AND verbal_symbolic skills.

jsfisher said:
Hmm, now how could we possibly evaluate the merits of Doron's claim? Oh, I know, we'd need to refer to the definition of limit....

Your definition of limit is closed under your verbal_symbolic_only skills.

jsfisher said:
Again, learn the meaning of words. "I approach the door" does not mean "I can't reach the door." The sloppy mistakes you continue to make, Doron, are a symptom of true crank.

You are truly closed under your verbal_symbolic_only skills, which naturally prevents from you to distinguish between "I approach the door" and "I actually reach the door."

jsfisher said:
Again, the only way to establish that would be to use the definition of limit. You continue to leap over that part so you can maintain your dislike for and misunderstanding of such a basic concept.

Basic concepts of the considered subject can't be archived by using verbal_symbolic_only skills.

jsfisher said:
Excellent. According to Doron, if f(x) = 2, then f(x) ≠ 2.

You have exceeded yourself, Doron. Well done!

Not even closer.

"If L=2, then f(x) ≠ L as x approaches a".

This true expression is easily known if one's visual_spatial AND verbal_symbolic skills are used, which is definitely not your case, jsfisher.

For example, here is actually the same subject, which your verbal_symbolic_only skills can't actually reach:

-----------------------------------------------------------
Here is the abstract taken from Philip J. Davis and James A. Anderson book called “Nonanalytic Aspects of Mathematics and Their Implication for Research and Education,” SIAM Review 21(1979), 112-117:

Abstract
In this paper we make a distinction between the practice of mathematics as it is usually presented--a logical chain of abstract, analytical reasoning from premises to conclusions--and how mathematics seems to be done in actuality--as a series of nonverbal, analog, often kinesthetic or visual insights. Mathematics in recent years has created a hierarchy with highly abstract, logical and symbolic material at the peak and with more geometrical, visual, and analog material held to be of lesser worth. We argue that humans are known to vary widely in their approaches to cognition and that the areas of the human brain specifically related to language and logical analysis seem to comprise only a part of the machinery of our intellect. We suggest that it would be wise for the practitioners of mathematics, and perhaps especially the students of mathematics to be aware of the very important nonverbal elements in mathematics. We feel that excessive emphasis on the abstract, analytic aspects of thought may have had deleterious effects on the profession and that a more appropriate balance, more in line with our cognitive endowment as humans, is desirable.
----------------------------------------------------------

The Real-line and non-local numbers

By using verbal_symbolic AND visual_spatial skills we get a one comprehensive framework.

For example, by Traditional Mathematics (which is mostly based on verbal_symbolic skills) 0.111...₂ = 0.999...₁₀ = 1 where 1 is the considered mathematical object (the number itself) and 0.111...₂ or 0.999...₁₀ are some numerals (out of many representations) that represent number 1.

By using verbal_symbolic and visual_spatial skills as follows:

[qimg]http://farm7.static.flickr.com/6142/5962015728_d2fe37cc5f_z.jpg[/qimg]

one understands that no branch of that tree actually reaches any other branch of that tree "downward" , no matter how many levels
that tree has (in other words, there is no homeomorphism between 0 dimensional space (notated by "0";"1" symbols)
and 1 dimensional space (notated by "_____" spatial non-composed object)).

According to this comprehensive framework 0.111...₂ is a number of its own < number 1 by 0.000...1₂ where the "...1" part
of that number is the irreducibility of ___ 1 dimensional space into 0 dimensional space (known as a point).

By using verbal_symbolic and visual_spatial skills one enables to distinguish between non-local numbers like 0.111...₂ or 0.000...1₂, and local numbers like 1.

Furthermore, no collection of, for example, 0 dimensional spaces along a 1 dimensional space has the power of the continuum of a 1 dimensional space.

By understanding the power of the continuum in terms of spatial skills, one understands that no collection of sub-objects of a given space (mathematical or physical) has the power of the continuum of that space, or in other words, any given collection of sub-objects is incomplete with respect to the "host" space.

The non-locality of 0.111...₂ or 0.000...1₂ is "naturally vague" in terms of location, and one actually discovers/invents that the Real-line has a non-empty set of non-strict numbers between 0 dimensional space and 1 dimensional space.

(By generalization, given a "host" space, no collection of "hosted" spaces has the power of the "host" space).

----------------------------------------------------------

doronshadmi · Sep 5, 2011

The Man said:
Doron, a single photon in impacts only a single spot on the screen.

Because the screen destroys the superposition of identities of the quantum objects.

The Man said:
Would a single photon impact on the screen be a “strict localization” or a “non-strict localization”?

Only “strict localization” because the screen destroys the superposition of identities of the quantum objects.

The Man said:
The distribution patterns you refer to are exactly that, the patterns of multiple photon impacts that are distributed over the screen. So now by your own assertions both your “non-strict localization” and “strict localization” are just distribution patterns.

The distribution patterns of "strict spots" is exactly the signature of the interaction among quantum objects, before they hit the screen and collapse into "strict spots". The distribution of wave patterns actually manifests the superposition of identities of the quantum objects before they hit the screen, where the distribution of a single peak pattern manifests the strict identities of the quantum objects before they hit the screen.

After all quantum objects are wavicles even if their wave properties and particle properties can't be manifested simultaneously.

The Man said:
Fine then show exactly how you “measure this spectrum” with your TURD, or stop lying.

TURD is your ill attitude of URDT, which is characterized by your "closed box" syndrome about this fine subject . As long as this is your initial attitude there is no use to talk with you about URDT.

Can you change your attitude about this fine subject?

The Man said:
doronshadmi said:

The non-locality is expressed as superposition of identities of the quantum objects, which has the symmetrical nature of wave patterns.

A gradual break of this symmetry provides the strict local nature of quantum objects as particles.

Click to expand...

Both the 50/50 and 0/100 distribution pattern examples in the link you cited are symmetrical (though about different axis). Please learn something (like what symmetrical means).

The Man, you defiantly have no clue about the symmetry of superposition of identities, because you do not distinguish, for example, between "AB" (which is an example of the symmetry among superposition of identities) and "A,B" (which is an example of the asymmetry among strict identities), exactly because your reasoning is closed under "A,B".

The Man said:
It that your problem that you just want to conflate symmetry breaking in your nonsense somewhere?

It that your problem that you just want to conflate symmetry by using your asymmetric "A,B"-only view?

The Man said:
The Schrödinger equation claims no such basis, stop lying Doron.

Once again, it can't claim such basis, exactly because it is the expression of "A,B"-only reasoning.

The Man said:
(“things are in many states until measured”)

It is not less than the symmetry of superposition of identities.

You can't comprehend that as long as you are closed under your asymmetric "A,B"-only reasoning.

The Man, you actually doing your best in order to stay closed under your asymmetric "A,B"-only reasoning all along this thread.

doronshadmi · Sep 5, 2011

Approach vs. reach:

http://www.usingenglish.com/forum/ask-teacher/27922-approach-vs-reach.html

Approach:

http://www.merriam-webster.com/dictionary/approach

http://dictionary.reference.com/browse/approach

http://en.wiktionary.org/wiki/approach

Reach:

http://dictionary.reference.com/browse/reach

http://www.thefreedictionary.com/reach

http://www.merriam-webster.com/dictionary/reach?show=0&t=1315216231

----------------------

http://en.wikipedia.org/wiki/Limit_of_a_function

In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input.

Informally, a function f assigns an output f(x) to every input x. The function has a limit L at an input p if f(x) is "close" to L whenever x is "close" to p. In other words, f(x) becomes closer and closer to L as x moves closer and closer to p. More specifically, when f is applied to each input sufficiently close to p, the result is an output value that is arbitrarily close to L.

To say that

$e30c17ced3a41ed9567363782e48d987.png$

means that ƒ(x) can be made as close as desired to L by making x close enough, but not equal, to p.

----------------------

In other words, jsfisher's community (which is based on verbal_symbolic_only skills) is wrong, formally and informally,
exactly because ƒ(x) ≠ L since x ≠ p.

jsfisher · Sep 5, 2011

doronshadmi said:
Approach vs. reach:
...
Approach:
...
Reach:

Doron, it doesn't matter one twit what you think the word, approach, should or should not mean in the limit definition. The fact remains, the definition itself tells us exactly what is meant by it.

Stop trying to disprove definitions. It cannot be done.

doronshadmi · Sep 5, 2011

jsfisher said:
Doron, it doesn't matter one twit what you think the word, approach, should or should not mean in the limit definition. The fact remains, the definition itself tells us exactly what is meant by it.

Stop trying to disprove definitions. It cannot be done.

Yavoll her jsfisher, the dictator of the mind.

jsfisher · Sep 5, 2011

doronshadmi said:
Yavoll her jsfisher, the dictator of the mind.

If you don't like all the definitions and such that make up Mathematics, go invent your own.

...Oh, yeah. You tried that. You couldn't come up with any workable definitions. In fact, nothing you tried led to anything other than the contradictory premises you started with.

Do let us know when you have some sort of useful result from Doronetics, won't you?

doronshadmi · Sep 5, 2011

jsfisher said:
If you don't like all the definitions and such that make up Mathematics, go invent your own.

...Oh, yeah. You tried that. You couldn't come up with any workable definitions. In fact, nothing you tried led to anything other than the contradictory premises you started with.

Do let us know when you have some sort of useful result from Doronetics, won't you?

Yavoll herr jsfisherr, the dictator of the mind.

The Man · Sep 5, 2011

doronshadmi said:
Because the screen destroys the superposition of identities of the quantum objects.

So now you are claiming that no interference pattern is ever visible on the screen?

doronshadmi said:
Only “strict localization” because the screen destroys the superposition of identities of the quantum objects.

Ah so now the double slit interference pattern on the screen is a “strict localization” since “screen destroys the superposition of identities of the quantum objects”.

doronshadmi said:
The distribution patterns of "strict spots" is exactly the signature of the interaction among quantum objects, before they hit the screen and collapse into "strict spots". The distribution of wave patterns actually manifests the superposition of identities of the quantum objects before they hit the screen, where the distribution of a single peak pattern manifests the strict identities of the quantum objects before they hit the screen.

Doron in a single shot double slit experiment there is no “interaction among quantum objects” as there is only one quantum (a single photon) per shot. The superposition is in the possible paths that single photon can take and not some “interaction among quantum objects”, which such single shot experiments clearly demonstrate. Though thank you once again for so obviously demonstrating that you understand absolutely nothing about double slit experiments.

What “distribution of wave patterns” are you referring to? “the distribution of a single peak pattern”?
Wouldn’t that make it a multiple peak pattern?

You seem to be confusing (again probably deliberately) a distribution pattern with some bizarre distribution of (a) pattern(s).

doronshadmi said:
After all quantum objects are wavicles even if their wave properties and particle properties can't be manifested simultaneously.

So this claim of yours before…

doronshadmi said:
The Man said:

Read about the uncertainty principle and learn why as what is considered a particle aspect becomes more defined (to a singular location) the wave aspect (frequency) becomes less defined and as the wave aspect becomes more defined (to a singular frequency) the particle aspect (location) becomes less defined. That’s duality Doron it always involves both.

Click to expand...

Indeed duality always involves both, such that it is changeable from 50%;50% which-way state (which is characterized by a wave pattern with non-strict localization) to 0%;100% which-way state (which is characterized by a single slit pattern with strict localization) by using partial measurements that are done between 50%;50% to 0%;100% , as shown, for example, in http://www.askamathematician.com/2011/06/q-what-is-a-measurement-in-quantum-mechanics/:

Was what, just another of your compulsive lies?

doronshadmi said:
TURD is your ill attitude of URDT, which is characterized by your "closed box" syndrome about this fine subject . As long as this is your initial attitude there is no use to talk with you about URDT.

Fine, you can stop talking about your TURD anytime you want, or can you?

doronshadmi said:
Can you change your attitude about this fine subject?

Can you demonstrate you can do what you claimed with your TURD or stop lying about it? Evidently not.

doronshadmi said:
The Man, you defiantly have no clue about the symmetry of superposition of identities, because you do not distinguish, for example, between "AB" (which is an example of the symmetry among superposition of identities) and "A,B" (which is an example of the asymmetry among strict identities), exactly because your reasoning is closed under "A,B".

You definitely still (and apparently deliberately) have no clue about the meaning of the word symmetry.

doronshadmi said:
It that your problem that you just want to conflate symmetry by using your asymmetric "A,B"-only view?

Nope, I have asserted no such view. In your previous post you attested to not only your knowledge that I have asserted no such view but also assert I “can't” even make such a claim.

doronshadmi said:
The Man said:

I have claimed no “"A,B"-only formal reasoning”.

Click to expand...

You can't because you are closed under it.

So in continuing to simply attempt to ascribe aspects of your own failed reasoning on to me you are just lying. Stop lying Doron.

doronshadmi said:
Once again, it can't claim such basis, exactly because it is the expression of "A,B"-only reasoning.

So now you attest to your knowledge that the Schrödinger equation makes no claim about being based “on strict variables” and also assert that it can make no such claim. So stop lying about it Doron.

doronshadmi said:
It is not less than the symmetry of superposition of identities.

Evidently even when your “superposition” (that you claim does not use superposition) is not even symmetrical.

doronshadmi said:
You can't comprehend that as long as you are closed under your asymmetric "A,B"-only reasoning.

The Man, you actually doing your best in order to stay closed under your asymmetric "A,B"-only reasoning all along this thread.

Stop lying Doron, by your own admission not only I have made no such assertions but in your opinion I can make no such assertions.

jsfisher · Sep 5, 2011

doronshadmi said:
Yavoll herr jsfisherr, the dictator of the mind.

Spell it properly, please. Also, please stop with the personal attacks. You are not advancing your argument one micron. The only thing you've done invoke Godwin's law.

doronshadmi · Sep 7, 2011

The Man said:
So now you are claiming that no interference pattern is ever visible on the screen?

No superposition of identities is shown on the screen, because it collapses into strict spots when hit the screen.

The Man said:
Ah so now the double slit interference pattern on the screen is a “strict localization” since “screen destroys the superposition of identities of the quantum objects”.

The wave pattern on the screen is not the superposition of identities.

Doron in a single shot double slit experiment there is no “interaction among quantum objects” as there is only one quantum (a single photon) per shot. The superposition is in the possible paths that single photon can take and not some “interaction among quantum objects”, which such single shot experiments clearly demonstrate. Though thank you once again for so obviously demonstrating that you understand absolutely nothing about double slit experiments.

The gap in time between shots has no influence on the superposition of identities in terms of space.

What “distribution of wave patterns” are you referring to? “the distribution of a single peak pattern”?
Wouldn’t that make it a multiple peak pattern?

There is the wave pattern and the peak(s) pattern(s).

The 50%;50% wave pattern is the signature of the superposition of identities, which is shown indirectly on the screen as a wave pattern of strict spots.

The 0;100% peak(s) pattern is the strict identities, which is shown directly on the screen as peak(s) of strict spots.

You seem to be confusing (again probably deliberately) a distribution pattern with some bizarre distribution of (a) pattern(s).

You seem to unable to get the difference between "AB" and "A,B", because all you get is in terms of "A,B".

The Man said:
So this claim of yours before…

Again, the screen detector destroys the superposition of identities, and as a result you always see strict spots on the screen, whether they are distributed as wave pattern or peak(s) pattern(s), and again, time has no influence of this result, because you get strict spots whether you shot many photons at the same time, or not.

The Man said:
Was what, just another of your compulsive lies?

No, it is you misunderstanding of the fact that the screen has an influence on the superposition of identities (the spots are always in strict positions, but there is a gradual change between the 50%;50% wave pattern of many strict spots, and the 0%;100% peak(s) pattern(s) of many strict spots).

The Man said:
You definitely still (and apparently deliberately) have no clue about the meaning of the word symmetry.

Again, The Man, you defiantly have no clue about the symmetry of superposition of identities, because you do not distinguish, for example, between "AB" (which is an example of the symmetry among superposition of identities) and "A,B" (which is an example of the asymmetry among strict identities), exactly because your reasoning is closed under "A,B".

The Man said:
Nope, I have asserted no such view.

Again, You can't because you are closed under it.

The Man said:
So in continuing to simply attempt to ascribe aspects of your own failed reasoning on to me you are just lying. Stop lying Doron.

This is all you are doing all along this thread, about this fine subject.

The Man said:
So now you attest to your knowledge that the Schrödinger equation makes no claim about being based “on strict variables” and also assert that it can make no such claim. So stop lying about it Doron.

The Man, by using only "in-the-box" reasoning, this reasoning can't deal also with "in-the-box" AND "out-of-the-box" reasoning.

The Man said:
Evidently even when your “superposition” (that you claim does not use superposition) is not even symmetrical.

Evidently your closeness under "A,B" can't comprehend "AB".

The Man said:
Stop lying Doron, by your own admission not only I have made no such assertions but in your opinion I can make no such assertions.

You are "in-the-box" The Man, and you are doing exactly nothing in order to also get out.

doronshadmi · Sep 7, 2011

jsfisher said:
Spell it properly, please. Also, please stop with the personal attacks. You are not advancing your argument one micron. The only thing you've done invoke Godwin's law.

jsfisher said:
Doron, it doesn't matter one twit what you think the word, approach, should or should not mean in the limit definition. The fact remains, the definition itself tells us exactly what is meant by it.

Stop trying to disprove definitions. It cannot be done.

jsfisher, you are indeed the dictator of the mind (your mind, in case you have missed it).

By this self dictatorship you are not advancing your ability to get http://www.internationalskeptics.com/forums/showpost.php?p=7540470&postcount=16339 and http://www.internationalskeptics.com/forums/showpost.php?p=7540060&postcount=16337.

jsfisher · Sep 7, 2011

doronshadmi said:
By this self dictatorship you are not advancing your ability to get....

Yeah, yeah. We've heard it all before. Your standard refrain when you muddle something and no one else agrees with you. It's everyone else's fault you don't understand simple concepts.

Well, at least I'm in great company. You, well, it must be very lonely for you. Also, my stuff works, producing remarkably useful results day after day. Do you have anything like that?

doronshadmi · Sep 8, 2011

jsfisher said:
Yeah, yeah. We've heard it all before.

And still you don't get it.

jsfisher said:
Do you have anything like that?

Do you have anything like http://www.internationalskeptics.com/forums/showpost.php?p=7511706&postcount=16304 ?

jsfisher said:
Well, at least I'm in great company.

It is a very dangerous company because it uses mind's skills in an imbalanced way, which has no ability to establish the unified basis of Logic AND Ethics.

jsfisher said:
Also, my stuff works, producing remarkably useful results day after day.

Your mind's self dictatorship can't comprehend the devastating results of your company's imbalanced expressions, which have no ability to actually establish the balanced scientific framework between Logic AND Ethics.

Again, I am talking about Ethics in evolutionary terms (which is not the narrow view of religious terms) , as can be seen, for example, in http://www.scribd.com/doc/16669828/EtikaE or http://www.scribd.com/doc/16547236/EEM .

jsfisher said:
You, well, it must be very lonely for you.

Your imbalanced company quickly lead us all to dead end street.

jsfisher, your mind's self dictatorship can't handle, for example, with http://www.internationalskeptics.com/forums/showpost.php?p=7548669&postcount=16347.

jsfisher · Sep 8, 2011

doronshadmi said:
...<nonsense snipped>...

My stuff still works. Demonstrable results day after day.

Why don't you have anything like that?

The Man · Sep 8, 2011

doronshadmi said:
No superposition of identities is shown on the screen, because it collapses into strict spots when hit the screen.

So you are claiming that no interference pattern would be visible on the screen? You do understand that the two single slit pattern is still a superposition just not an interference between those two slits, don't you?

doronshadmi said:
The wave pattern on the screen is not the superposition of identities.

The pattern on the screen is the superposition of the photon impacts. Where each photon is likely to impact is the result of the superposition of the possible paths it can take. Exactly what your “superposition of identities” means you have yet to verify other then it is expressly (by you) not a superposition.

doronshadmi said:
The gap in time between shots has no influence on the superposition of identities in terms of space.

What “identities”? The point of the single shoot experiments is to show that the interference is from the superposition of the possible paths for each photon and not a result of the interaction of multiple photons.

doronshadmi said:
There is the wave pattern and the peak(s) pattern(s).

They are distribution patterns and either could be the pattern of some wave.

doronshadmi said:
The 50%;50% wave pattern is the signature of the superposition of identities, which is shown indirectly on the screen as a wave pattern of strict spots.

The distribution patterns show directly on the screen (double, single slit and two single slits). The double slit interference patterns show the superposition of the possible paths, including the 15/85 and 1/99 patterns cited in the reference you provided. However, as noted before only the 50/50 and 0/100 patterns are symmetrical.

doronshadmi said:
The 0;100% peak(s) pattern is the strict identities, which is shown directly on the screen as peak(s) of strict spots.

“the strict identities”? What are these “strict identities”? Please specificly identify these “strict identities” which should not be a problem for you as you have claimed they are “identities” and that they are, well, “strict”.

doronshadmi said:
You seem to unable to get the difference between "AB" and "A,B", because all you get is in terms of "A,B".

You are demonstrably unable to cite any difference between your "AB" and your "A,B", because you will refuse to confirm or will directly contradict any difference you previously claim.

doronshadmi said:
Again, the screen detector destroys the superposition of identities, and as a result you always see strict spots on the screen, whether they are distributed as wave pattern or peak(s) pattern(s), and again, time has no influence of this result, because you get strict spots whether you shot many photons at the same time, or not.

What “identities”? What “superposition”? By you own assertion there is no superposition in your “superposition”. How does the detector destroy a “superposition” that you claim involves no superposition (looks like you destroyed that yourself)? Exactly how “strict” are these spots of yours.

doronshadmi said:
No, it is you misunderstanding of the fact that the screen has an influence on the superposition of identities (the spots are always in strict positions, but there is a gradual change between the 50%;50% wave pattern of many strict spots, and the 0%;100% peak(s) pattern(s) of many strict spots).

Nope just your deliberate misunderstanding as usual since your “superposition of identities” doesn’t (by your own assertion) involve any superposition. It would seem you’re the only one who can influence your “superposition of identities”. Again, clearly identify your “identities” and your “superposition” as you claim it does not involve superposition.

doronshadmi said:
Again, The Man, you defiantly have no clue about the symmetry of superposition of identities, because you do not distinguish, for example, between "AB" (which is an example of the symmetry among superposition of identities) and "A,B" (which is an example of the asymmetry among strict identities), exactly because your reasoning is closed under "A,B".

Again learn what symmetry means Doron. Your own cited reference shows two slit interference patterns that are not symmetrical. I’m sure no one here is surprised to find that your “symmetry of superposition of identities”, which you claim does not involve superposition, also lacks symmetry as well as apparently any identities.

doronshadmi said:
Again, You can't because you are closed under it.

So stop lying about it.

doronshadmi said:
This is all you are doing all along this thread, about this fine subject.

Stop lying Doron, I have never tried to ascribe any kind of reasoning to you.

doronshadmi said:
The Man, by using only "in-the-box" reasoning, this reasoning can't deal also with "in-the-box" AND "out-of-the-box" reasoning.

Evidently your closeness under "A,B" can't comprehend "AB".

You are "in-the-box" The Man, and you are doing exactly nothing in order to also get out.

Again stop simply trying to posit aspects of your own failed reasoning onto others.

doronshadmi · Sep 9, 2011

The Man said:
So you are claiming that no interference pattern would be visible on the screen? You do understand that the two single slit pattern is still a superposition just not an interference between those two slits, don't you?

The Man said:
The pattern on the screen is the superposition of the photon impacts. Where each photon is likely to impact is the result of the superposition of the possible paths it can take. Exactly what your “superposition of identities” means you have yet to verify other then it is expressly (by you) not a superposition.

The wave pattern of strict spots on the screen is an indirect expression of the superposition of identities. As long as you get "AB" in terms of "A,B" you can't get that.

What “identities”? The point of the single shoot experiments is to show that the interference is from the superposition of the possible paths for each photon and not a result of the interaction of multiple photons.

What you call "each photon" is understood by you only in terms of strict identity, which is derived from a strict location on the screen. Since this is all you get, you indeed ask

The Man said:
What “identities”?

Again it is shown that your understanding of quantum objects is limited only to Locality (the non-local property (superposition of identities) of a quantum object is not understood by you).

The Man said:
They are distribution patterns and either could be the pattern of some wave.

The distribution patterns show directly on the screen (double, single slit and two single slits). The double slit interference patterns show the superposition of the possible paths, including the 15/85 and 1/99 patterns cited in the reference you provided. However, as noted before only the 50/50 and 0/100 patterns are symmetrical.

All there is on the screen is different patterns of strict spots.

The Man said:
What “identities”? What “superposition”? By you own assertion there is no superposition in your “superposition”. How does the detector destroy a “superposition” that you claim involves no superposition (looks like you destroyed that yourself)? Exactly how “strict” are these spots of yours.

Symmetry actually exists as long as a superposition of identities is not changed into strict identities, where strict identities appear as strict spots on the screen. You still do not get that the screen has an influence on the result of the double silts experiment, no matter if you are using a "which-way" measurement, or not.

The Man said:
“the strict identities”? What are these “strict identities”? Please specificly identify these “strict identities” which should not be a problem for you as you have claimed they are “identities” and that they are, well, “strict”.

Each spot on the screen has a strict identity ("AB" is changed into "A" or "B", where "A" or "B" are strict identities of "A,B" collection).

The Man said:
You are demonstrably unable to cite any difference between your "AB" and your "A,B", because you will refuse to confirm or will directly contradict any difference you previously claim.

The Man, your "A,B"-only reasoning prevents the understanding of URDT ( http://www.internationalskeptics.com/forums/showpost.php?p=7511706&postcount=16304 ).

The Man said:
Nope just your deliberate misunderstanding as usual since your “superposition of identities” doesn’t (by your own assertion) involve any superposition. It would seem you’re the only one who can influence your “superposition of identities”. Again, clearly identify your “identities” and your “superposition” as you claim it does not involve superposition.

Well, is is strictly known that you can't get “superposition of identities”.

The Man said:
Again learn what symmetry means Doron. Your own cited reference shows two slit interference patterns that are not symmetrical. I’m sure no one here is surprised to find that your “symmetry of superposition of identities”, which you claim does not involve superposition, also lacks symmetry as well as apparently any identities.

Learn how to get thing not only in terms of "A,B"-reasoning.

The Man said:
So stop lying about it.

Stop lying to yourself by limit it only to "A,B"-reasoning.

The Man said:
Stop lying Doron, I have never tried to ascribe any kind of reasoning to you.

Ho yes are forcing your "A,B"-only reasoning all along this thread, exactly because "A,B" is all you can get.

The Man said:
Again stop simply trying to posit aspects of your own failed reasoning onto others.

You do not need me The Man, you actually doing the job by yourself by limit it to only to "A,B"-reasoning.

doronshadmi · Sep 9, 2011

jsfisher said:
My stuff still works. Demonstrable results day after day.

Why don't you have anything like that?

http://www.internationalskeptics.com/forums/showpost.php?p=7550576&postcount=16349.

jsfisher · Sep 9, 2011

doronshadmi said:
http://www.internationalskeptics.com/forums/showpost.php?p=7550576&postcount=16349.

So, that's your response to whether you have anything the works. You could have just said "No". There was no need for the URL.

doronshadmi · Sep 9, 2011

jsfisher said:
So, that's your response to whether you have anything the works. You could have just said "No". There was no need for the URL.

For your self-dictatorship of your mind, you indeed get nothing of http://www.internationalskeptics.com/forums/showpost.php?p=7550576&postcount=16349.

The Man · Sep 9, 2011

doronshadmi said:
The wave pattern of strict spots on the screen is an indirect expression of the superposition of identities. As long as you get "AB" in terms of "A,B" you can't get that.

Again, what “identities”? We already know by your own assertion there is no superposition in your “superposition”.

doronshadmi said:
What you call "each photon" is understood by you only in terms of strict identity, which is derived from a strict location on the screen. Since this is all you get, you indeed ask

What the heck are you babbling about now? You should probably look up what the word photon means.

doronshadmi said:
Again it is shown that your understanding of quantum objects is limited only to Locality (the non-local property (superposition of identities) of a quantum object is not understood by you).

Once again you simply choose to lie by calling your “superposition” precisely what you claim it does not involve, superposition. Stop lying Doron.

doronshadmi said:
All there is on the screen is different patterns of strict spots.

Again exactly how “strict” are these “spots” of yours?

doronshadmi said:
Symmetry actually exists as long as a superposition of identities is not changed into strict identities, where strict identities appear as strict spots on the screen. You still do not get that the screen has an influence on the result of the double silts experiment, no matter if you are using a "which-way" measurement, or not.

I’m sure it surprises no one that your “symmetry” does not involve, well, symmetry.

doronshadmi said:
Each spot on the screen has a strict identity ("AB" is changed into "A" or "B", where "A" or "B" are strict identities of "A,B" collection).

So as expected your “strict identities” don’t even invole any identites (strict or otherwise).

doronshadmi said:
The Man, your "A,B"-only reasoning prevents the understanding of URDT ( http://www.internationalskeptics.com/forums/showpost.php?p=7511706&postcount=16304 ).

Stop lying Doron, you have attested to your knowledge that I have claimed no “"A,B"-only reasoning” and further asserted your opinion that I can not even make such a claim.

doronshadmi said:
Well, is is strictly known that you can't get “superposition of identities”.

That would be your “superposition” without superposition and those “identities” you evidently just couldn’t identify? We got that some time ago.

doronshadmi said:
Learn how to get thing not only in terms of "A,B"-reasoning.

Stop lying Doron, you have attested to your knowledge that I have claimed no “"A,B"-only reasoning” and further asserted your opinion that I can not even make such a claim.

doronshadmi said:
Stop lying to yourself by limit it only to "A,B"-reasoning.

I have attributed and limited nothing “only to "A,B"-reasoning”, While you have attested to your knowledge that I have claimed no “"A,B"-only reasoning” and further asserted your opinion that I can not even make such a claim. So stop lying Doron

doronshadmi said:
Ho yes are forcing your "A,B"-only reasoning all along this thread, exactly because "A,B" is all you can get.

Who are you calling a “Ho”?

Show specifically where I have ascribed any kind of reasoning to you or stop lying about it.

Stop lying Doron, you have attested to your knowledge that I have claimed no “"A,B"-only reasoning” and further asserted you opinion that I can not even make such a claim.

doronshadmi said:
You do not need me The Man, you actually doing the job by yourself by limit it to only to "A,B"-reasoning.

I have certainly never asserted any need for you Doron and I have never claimed any “"A,B"-only reasoning”. You however have attested to your knowledge that I have claimed no “"A,B"-only reasoning” and further asserted your opinion that I can not even make such a claim. So stop lying Doron, but evidently you simply can't.

jsfisher · Sep 9, 2011

doronshadmi said:
For your self-dictatorship of your mind, you indeed get nothing of http://www.internationalskeptics.com/forums/showpost.php?p=7550576&postcount=16349.

Result, you need to produce an actual result. Simply saying where you think your incredible dearth might apply is not a result.

doronshadmi · Sep 10, 2011

jsfisher said:
Result, you need to produce an actual result. Simply saying where you think your incredible dearth might apply is not a result.

An actual result is a new understanding of the considered subject.

doronshadmi · Sep 10, 2011

The Man said:
Again, what “identities”?

The Man, have a pleasant life in your strict box, I am not going to continue the discussion on this fine subject with you.

epix · Sep 10, 2011

doronshadmi said:
The Man, have a pleasant life in your strict box, I am not going to continue the discussion on this fine subject with you.

The unfolding of your words gives light; it gives understanding to the simple.
Psalm 119:130

I didn't know that you also venture beyond "local" Devarim.

Deeper than primes

ETcorngods survivor

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

ETcorngods survivor

ETcorngods survivor

Penultimate Amazing

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

ETcorngods survivor

Unbanned zombie poster

Penultimate Amazing

Penultimate Amazing

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

Unbanned zombie poster

ETcorngods survivor

Penultimate Amazing

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

ETcorngods survivor

Unbanned zombie poster

Penultimate Amazing

Penultimate Amazing

ETcorngods survivor

Penultimate Amazing

Unbanned zombie poster

ETcorngods survivor

Penultimate Amazing

Penultimate Amazing

Banned