Deeper than primes - Continuation

Status
Not open for further replies.
doronshadmi said:
The traditional mathematicians here still avoiding http://www.internationalskeptics.com/forums/showpost.php?p=8688490&postcount=2039, simply because they have no argument as long as they are using only their verbal_symbolic brain skills.
Click to expand...


It's that reading comprehension thing, again, isn't Doron? With a little professional help, you could make great improvement.

Actually, a reasonable exercise for you right now would be to re-read what's been posted recently until you do understand that (1) your post had a blunder-rich foundation, and (2) you are yet again trying to disprove definitions. (Definitions continue to be exempt from proofs and disproofs.)

Still sucks to be you, Doron. Mathematics isn't simply what you want it to be. If it is any consolation, you can have your own private definition that behaves more the way you imagine it should. We can call it the Doron-circle. It just needs you to define it. I'm sure you will find great utility for your Doron-circle over the regular kind.
 
Last edited:
doronshadmi said:
Definitions continue not to be exempt from re-consideration if only partial brain skills are used to express and use them.
Click to expand...

I completely agree, but this bit of near gibberish does not express what you think it does. Quite the opposite, in fact.

Once again the traditional mathematician here simply avoids http://www.internationalskeptics.com/forums/showpost.php?p=8688490&postcount=2039.
Click to expand...

Repeating your lie does make it true, only more of a lie.

The main argument is found in http://www.internationalskeptics.com/forums/showpost.php?p=8686803&postcount=2032.
Click to expand...

Your main argument simply expands your blunder base.

Do you have a point, by the way? You don't like degenerate circles, we get that, but so what? You don't like them; the definition allows them. Why this long, tortured excursion into Doron-nonsense? Time to move on.

How about we just accept Doron-circles as defined, even without you having to define them. Now what?
 
Some given phrase of a traditional mathematician:

"You don't like degenerate circles, we get that, but so what? You don't like them; the definition allows them."

It is "nice" isn't it? A definition of circles that was done by traditional mathematicians provides degenerate circles, but there is no problem because definitions are not re-considered by traditional mathematicians even if they allow degenerate objects.

At least it becomes clear why the traditional mathematician here can't deal with http://www.internationalskeptics.com/forums/showpost.php?p=8686803&postcount=2032.

According to the same reasoning, as expressed above by some traditional mathematician, 1-dimensional space has exactly 0 length, or 0-dimensional space has some length > 0 just because some mathematician expressed some definition.

Such arguments simply expands the traditional mathematicians' blunder base, and clearly show why developments like Organic Mathematics ( http://www.internationalskeptics.com/forums/showpost.php?p=8679690&postcount=2022 ) are needed.
 
Last edited:
doronshadmi said:
It is "nice" isn't it? A definition of circles that was done by traditional mathematicians provides degenerate circles
Click to expand...

Many definitions admit degenerate cases. A degenerate ellipse is a circle. Do you have a problem with that, too? You have yet to show an particular problem the standard geometry definition for circle creates other than your dislike.

...but there is no problem because definitions are not re-considered by traditional mathematicians even if they allow degenerate objects.
Click to expand...

Not true. Definitions in Mathematics are introduced for their lexical convenience. Degenerate cases can be included or excluded as common usage would find more convenient.

You have failed to show any inconvenience the definition for circle creates, let alone a compelling inconvenience.

At least it becomes clear why the traditional mathematician here can't deal with http://www.internationalskeptics.com/forums/showpost.php?p=8686803&postcount=2032.
Click to expand...

A lie repeated is still a lie.

Enough with your silly bluster. If you have anything real to say do so, but your continued empty denial of how real Mathematics works only highlights your ignorance. Nothing more.
 
doronshadmi said:
Here is an example of verbal_symbolic-only reasoning.

Definition of Circle

Definition: A circle is the set of all points that are the same distance, r, from a fixed point.

General Formula: X2 + Y2 = r2 where r is the radius.

According to this verbal_symbolic-only reasoning, we still have a circle even if r=0 or r=∞, which is simply nonsense.
Click to expand...
The way you convey your thoughts about the circle strongly suggests that you never attempted to draw one using other means than a compass. Here are a few arguments that tend to support my claim.

Start with the implicit equation that defines the unit circle:

x2 + y2 = 1

The presence of x and y in the equation tells you that the circle will be drawn with the help of Cartesian coordinates and the equation assumes that the center of the unit circle is at x=0 and y=0. The presence of both variables also tells you that it is a function that will draw the circle.

Since 1 = 12, you can rewrite the equation this way:

x2 + y2 = 12
A "unit circle" means that the radius of it equals 1, or r = 1. That definition rewrites the above equation to the form that you presented:

x2 + y2 = r2
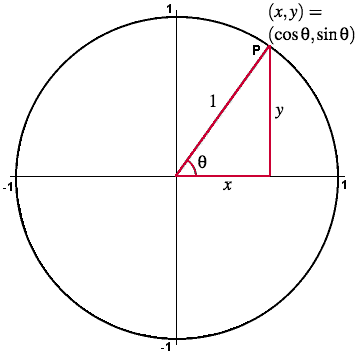
You see (or you should) that the equation strongly resembles Pythagorean theorem. Just consider the radius as the hypothenuse of the right-angle triangle where the hypothenuse has a constant length (h =1). Now call upon your visual_spatial brain skills to see how the circle will be drawn.

250px-Cartesian-coordinate-system-with-circle.svg.png


The pic shows a circle with r = 2.. Since the implicit equation cannot do the job of drawing the circle, you need to convert it into its explicit form to separate the independent variable x from the dependent variable y. You will basically compute the length of the y-side of the right-angle triangle within the circle according to the given x-side whose length varies.

y = √(r2 - x2)

ucdefp.gif


The function f(x) = y will draw a set of points where the set is defined as Semicircle. (You can't draw a full circle using only one function in the Cartesian coordinate system.)

Now here is once again your assertion:

General Formula: X^2 + Y^2 = r^2 where r is the radius.

According to this verbal_symbolic-only reasoning, we still have a circle even if r=0 or r=∞, which is simply nonsense.
Click to expand...

Since r=∞ is an illegal definition given the way you wrote the implicit equation, you can use the other option, where the radius is zero, and do the substitution within the function (r2 = 02 = 0).

y = √(0 - x2) = √(- x2)

Remember that - x2 = - (x2). Since there is no real result to the square root of any negative number, the circle cannot be drawn when r=0. In other words, "we still have a circle" NOT. That's how math works: just follow the rules and hope for the best.

But when Man decides that he wants that circle, he will have it no matter what. There is a magic letter that can be added to the equation where the radius is zero and the circle will exist pretty, even though it actually doesn't exist on a differently defined plane - the one that is closer to the real world around us. What is the magic letter that you stick into the function right after the x, Doron?

Here is a clue: the magic letter is the first in a word that describes your attitude toward simple proofs the best.
 
Last edited:
Now we can see that according to Traditional Mathematics' reasoning 0-dimesional space can be defined as degenerate 1-dimesional space (or vice versa, it does not matter), because after all many degenerate (and I would simply say inconsistent) objects are defined by the group of people that are called traditional mathematicians.

In other words, we deal here with a framework where inconsistency is its inherent property in too many cases.

When these inconsistencies are exposed, we realize that we deal with fanatic group of people that instead of re-considering these inconsistencies in order to fix them, they prefer to warship their own inconsistent definitions.

There is no wonder that there cannot be any fruitful communication between those who expose these inconsistencies and this fanatic group of people.

------------------

According to Organic Mathematics reasoning, by using also visual_spatial brain skills, one easily understands that an expression like 0 = X2 + Y2 is not some case of degenerate circle, but it is simply the indivisible local building-block (0-dimensional space, in this case), where an expression like ∞ = X2 + Y2 is not some case of degenerate circle, but it is simply the indivisible non-local building-block (1-dimensional space, in this case), such that if these building-blocks are associated, they provide a given circle (where the position of that circle on a given plane (real, complex or whatever) has no influence on the validity of the considered novel notion, which fixes the inconsistent notion of degenerate circles).

------------------

Generally, the tolerance of traditional mathematicians to inconsistent objects that are provided by their definitions, actually prevents the development of the mathematical science beyond its current entropic-oriented state.

More about entropic-free realm can be seen, for example, in:

http://www.internationalskeptics.com/forums/showpost.php?p=8636880&postcount=1984

http://www.internationalskeptics.com/forums/showpost.php?p=8679690&postcount=2022
 
Last edited:
Look at this phrase:

"Since there is no real result to the square root of any negative number, the circle cannot be drawn when r=0."

A circle is the set of all points (there must be more than one point) on a given plane, which are at the same distance, r, from a fixed point, where the given plane is not restricted to the universe of real numbers, and the position the circle on the considered plane is insignificant.

Some posters here do not understand these simple facts.
 
Last edited:
Little 10 Toes said:
For what? Pointing out your errors? I'm just one of many. I play a minor role in pointing out your major errors.
Click to expand...
So what exactly do you wish to express by writing
Little 10 Toes said:
..., I will respond to your reply to me. ...
Click to expand...
?


Little 10 Toes said:
By the way, do you know what imaginary numbers are?
Click to expand...

Little 10 Toes, I am talking also about circles on the complex plane, which is the mathematical universe of imaginary numbers, so your questions are irrelevant in this case.
 
Last edited:
doronshadmi said:
A Doron-circle is the set of all points (there must be more than one point) on a given plane, which are at the same distance, r, from a fixed point, where the given plane is not restricted to the universe of real numbers, and the position the circle on the considered plane is insignificant.
Click to expand...

Ah! So we have your version, finally, of what how 'circle' should be defined. Remarkably wordy and filled with the extraneous, but better than I expected.

It is interesting that you, Doron, consider the center insignificant. Real Mathematics makes the reference plane, radius, and center all significant, but not doronetics.

A bold move on your part, Doron, but just how is this departure from sanity useful?
 
The position of a circle on a given plane is insignificant if we wish to understand the involved building-blocks, which are not themselves circles (to call them degenerate circles does not help to understand these building-blocks and the results of their possible associations as valid circles (a circle is valid if Pi is actually found).

B.T.W it is possible to define infinity many valid circles, by using an infinitely long cone that crosses infinitely many planes, such that its central axis is perpendicular w.r.t them , for example:

er7628a9b5hoeksd.jpg

http://archinect.com/blogs/gallery/27837500/0/exile-and-the-sun-future-light-cones

Also in this case the two mentioned building-blocks (1-dimensional space and 0-dimensional space, where no one of them is a valid circle) are involved, where in this case "the game of valid circles" takes place in 2 and 3 dimensional spaces.
 
Last edited:
doronshadmi said:
The position of a circle on a given plane is insignificant if we wish to understand the involved building-blocks, which are not themselves circles (to call them degenerate circles does not help to understand these building-blocks and the results of their possible acclamations as valid circles
Click to expand...

Gibberish.

(a circle is valid if Pi is actually found).
Click to expand...

I was unaware pi was missing. Was this a recent development?

B.T.W it is possible to define infinity many valid circles, by using an infinitely long cone that crosses infinitely many planes that are perpendicular w.r.t its central axis, for example:

[qimg]http://cdn.archinect.net/images/650x/er/er7628a9b5hoeksd.jpg[/qimg]
Click to expand...


Excellent!! Classic self-contradiction, Doron. You endorse an example that includes the very thing you are trying to banish. Well done. It's the moments like these that make this thread so entertaining.
 
Unfortunately the traditional mathematician here (Gibberish is the best he can get, in this case, because a post like http://www.internationalskeptics.com/forums/showpost.php?p=8690349&postcount=2048 is beyond his entropic-oriented reasoning) still does not understand that the infinitely long 1-dimensional spaces are one type of the two building-blocks (the other type is 0-dimensional space), which are not themselves circles but they enable the infinitely many valid circles (where a circle is valid only if Pi is found).
 
Last edited:
doronshadmi said:
Unfortunately the traditional mathematician here (Gibberish is the best he can get, in this case, because a post like http://www.internationalskeptics.com/forums/showpost.php?p=8690349&postcount=2048 is beyond his entropic-oriented reasoning) still does not understand that the infinitely long 1-dimensional spaces are one type of the two building-blocks (the other type is 0-dimensional space), which are not themselves circles but they enable the infinitely many valid circles (where a circle is valid only if Pi is found).
Click to expand...

Try thinking before you respond. Your example contains a circle with r=0, you said it was not a circle.
 
doronshadmi said:
Look at this phrase:

"Since there is no real result to the square root of any negative number, the circle cannot be drawn when r=0."

A circle is the set of all points (there must be more than one point) on a given plane, which are at the same distance, r, from a fixed point, where the given plane is not restricted to the universe of real numbers, and the position the circle on the considered plane is insignificant.

Some posters here do not understand these simple facts.
Click to expand...
Speaking of simple facts... You blessed the board with an implicit equation that defined a circle drawn on the real plane and then you accused the traditional mathematicians of being capable of drawing that circle when it is in its degenerate form, meaning its radius equals zero or infinity.

General Formula: X^2 + Y^2 = r^2 where r is the radius.

According to this verbal_symbolic-only reasoning, we still have a circle even if r=0 or r=∞, which is simply nonsense.
Click to expand...

Due to your high school math illiteracy, and unlike the squirrel that gets in through the open kitchen windows to steal my peanuts, you couldn't follow the proof of your statement being false.
http://www.internationalskeptics.com/forums/showthread.php?postid=8689234#post8689234

1) Real algebra doesn't allow infinity to join the set of real numbers and therefore the traditional mathematician couldn't define radius as r=∞. But since you and the literal creationists share the space in the same box, you keep making attributes that are patently false. I found it rather amusing, because when someone starts only to question the numbers that made up Holocaust, you would be the first one to cock the gun.

2) Real algebra has its rules and when they are applied in connection with a circle where r=0, then the circle cannot be drawn. But you claimed, and would continue to do so, that according to those degenerate (pun intended) traditional mathematicians "we still have a circle."

The circle is often used as a symbol describing round objects, such as the human head. In that case, the term "degenerate circle" doesn't refer to the radius extrema but to something else. So it's not a surprise that your mind is capable of coming up with a circle whose properties would baffle anyone else belonging to Kingdom Animalia.
 
sympathic said:
Your example contains a circle with r=0, you said it was not a circle.
Click to expand...
Your wrong interpretation of my example contains a valid circle with r=0.

Once again, a valid circle is defined as the set of all points (there must be more than one point) on a given plane, which are at the same distance, r, from a fixed point, where the given plane is not restricted to the universe of real numbers, the position of the circle on the considered plane is insignificant and Pi must be found.

Any other attempt that does not follow these rules, can't provide a valid circle.
 
Last edited:
doronshadmi said:
I am an evolutionist, as clearly can be understood by any one who really reads http://www.internationalskeptics.com/forums/showpost.php?p=8636880&postcount=1984 and http://www.internationalskeptics.com/forums/showpost.php?p=8675409&postcount=2014 posts.
Click to expand...
Literal creationists accuse evolutionary scientists from making trivial mistakes that they never did. You follow suit except your target are mathematicians, and so the links to the chair which you think you're sitting on are waste of the mouse.
 
Traditional Mathematicians are definitely anti-evolutionists exactly because they reject any re-considerations (and I would say mutations) of their definitions etc.

Examples of such rejections are found all along this thread.

Here is some example:

I "have failed to show any inconvenience the definition for circle creates, let alone a compelling inconvenience" exactly because traditional mathematicians do not care about degenerate (invalid) objects that are provided by their definitions.

Instead of re-consider such definitions they claim that "Definitions in Mathematics are introduced for their lexical convenience" (this is an example of how verbal_symbolic-only reasoning works), where "Degenerate cases can be included or excluded as common usage would find more convenient".

It is indeed more convenient (for lazy traditional minds) to avoid re-considerations of definitions that provide degenerate cases, because one has to be developed beyond the tolerance to degenerate cases in order to fix these cases by using better notions.

The better notions, this case, is that 1-dimesional space and 0-dimensional space are the indivisible building-blocks (which are not themselves circles) that if associated, they are able to provide any possible valid circle ( http://www.internationalskeptics.com/forums/showpost.php?p=8691969&postcount=2062 ).

Let us address it this way: According to Traditional Mathematics' reasoning since "Definitions in Mathematics are introduced for their lexical convenience", then there is no problem (by considerations of lexical convenience) to define not not as a degenerate case of not and then to claim that there is no significant difference between not not and not (again, by considerations of lexical convenience).
 
Last edited:
doronshadmi said:
Your wrong interpretation of my example contains a valid circle with r=0.
Click to expand...

You are mistaken. Your example includes a circle of zero radius, the very thing you dislike so much.

Once again, a valid circle is defined as the set of all points (there must be more than one point) on a given plane, which are at the same distance, r, from a fixed point, where the given plane is not restricted to the universe of real numbers, the position of the circle on the considered plane is insignificant and Pi must be found.
Click to expand...


Nope. That may be something that approximates the definition for the elusive Doron-circle, but circles have a simpler definition.

Oh, and since you are having such trouble with this pi side issue, have a look between omicron and rho. Pi is completely safe and hasn't moved from that location in quite a long time. You can call off the search party.
 
doronshadmi said:
Traditional Mathematicians are definitely anti-evolutionists exactly because they reject any re-considerations (and I would say mutations) of their definitions etc....
Click to expand...


More nay saying, eh? Since you can do nothing constructive with doronetics, you try to ridicule that which you do not understand.

If we could move beyond the playground taunts, the out-and-out lies, the gibberish, the contradictions, the straw men, the logic failures, and all that, it would be great!

Meanwhile, my stuff still works; yours, nope.
 
doronshadmi said:
The agreements between traditional mathematicians are not going to eliminate what is written in http://www.internationalskeptics.com/forums/showpost.php?p=8692222&postcount=2065.
Click to expand...

Why would anyone want to eliminate it? It's pure comedy gold!

Since this is the case Traditional Mathematics (as it is currently done) is not going to be a part of future development of the mathematical science.
Click to expand...

Have you considered applying for the MDC? With predictions like that, you'd be a shoo-in. You just need a time frame for your prophecies so they would be testable.
 
doronshadmi said:
The position of a circle on a given plane is insignificant if we wish to understand the involved building-blocks, which are not themselves circles (to call them degenerate circles does not help to understand these building-blocks and the results of their possible associations as valid circles (a circle is valid if Pi is actually found).

B.T.W it is possible to define infinity many valid circles, by using an infinitely long cone that crosses infinitely many planes, such that its central axis is perpendicular w.r.t them , for example:

[qimg]http://cdn.archinect.net/images/650x/er/er7628a9b5hoeksd.jpg[/qimg]
http://archinect.com/blogs/gallery/27837500/0/exile-and-the-sun-future-light-cones

Also in this case the two mentioned building-blocks (1-dimensional space and 0-dimensional space, where no one of them is a valid circle) are involved, where in this case "the game of valid circles" takes place in 2 and 3 dimensional spaces.
Click to expand...
You draw inspiration from very speculative and therefore unproven stuff. After "doronizing" it, the result is a set of phantasmagoric propositions.

Speaking of a set... The radius line is a line segment of a given length that can be uniformly extended in both directions. If you consider line segment [a, b], where a<b and you are extending into the positive territory by moving point b, the process is allowed to continue unbound, because it preserves the definition of the line segment. But moving point b in the opposite direction poses a problem, because it will encounter point a. That would cause a collision that looks like this: a = b. The consequence is that the line segment has now only one point and that seemingly defeats the applicable part of the definition:

In geometry, a line segment is a part of a line that is bounded by two end points...

Since the consequence of a = b is a - b = 0, one might argue that a and b are the end points of a line segment whose length is zero, and the definition stipulating the presence of two points stands. But how do both points coexist? There are two points that share the same location and that exclude them from being admitted to the set theory where members of a set cannot engage in a relationship, such as a = b. (Thou shall not...) But nowadays almost any math issue is considered from the prospect of the set theory to avoid lexical inconsistencies. So what's the fate of a line segment whose length equals zero? As the Chief Arbiter of the Final and Inappealable Judgement, you ought to slam the judicial hammer on the issue.
 
Look at this claim: "You draw inspiration from very speculative and therefore unproven stuff".

What's actually going on is this:

Traditional mathematicians have no problem to define degenerate cases that are provided by their definitions because (according to traditional mathematicians) "Definitions in Mathematics are introduced for their lexical convenience" (this is an example of how verbal_symbolic-only reasoning works).
 
doronshadmi said:
Traditional mathematicians have no problem to define degenerate cases that are provided by their definitions
Click to expand...

This seems to confuse you. Perhaps if you'd stop conflating "degenerate case" with "invalid case" you'd lessen your own confusion. Not all things that share one property (e.g. being a circle) have all the same other properties. Zero is an integer, yet zero is degenerate with respect to division. In doronetics, is zero therefore invalid as an integer?

...because (according to traditional mathematicians) "Definitions in Mathematics are introduced for their lexical convenience" (this is an example of how verbal_symbolic-only reasoning works).
Click to expand...

So, in doronetics definitions are introduced for their lexical inconvenience. Yes, that has been apparent.
 
Let's look at this phrase: "Not all things that share one property (e.g. being a circle) have all the same other properties."

It is true, but there are properties that if they are not related to a given thing it can't be considered as this thing anymore, for example:

1. An empty set that has more than 0 members.

2. A circle without Pi.

etc. ...

If we use considerations that are derived from, so called, "lexical convenience" (for example: "an object with 0-dimesional space (a point) is a degenerate circle" or "the empty set is a degenerate case of non-empty set" or "not not is a degenerate case of not") we actually force indistinguishably between different things, in order to save the, so called, "lexical convenience".

The level of Polychotomy is characterized by the difference between things, which is derived by, at least, verbal_symbolic AND visual_spatial brain skills, where "lexical convenience" is derived only from verbal_symbolic brain skills (and as a result it is not powerful enough to distinguish between things that are recognized by verbal_symbolic AND visual_spatial brain skills).

Moreover, the traditional mathematicians understand Abstraction only in terms of verbal_symbolic brain skills.

Furthermore, they claim that the defined abstract objects are independent of the mathematician's brain skills (B.T.W in that case a phrase like "lexical convenience" has no meaning).

By taking this road they do not understand that Life is a natural development of a given realm to be aware of itself, where this self-awareness is the development of the unaware mutual influence between, for example, a falling tree and the ground.

Reasoning that is derived only from verbal_symbolic brain skills (which are motivated by "lexical convenience" considerations) can't be considered as a satisfactory foundation for The Mathematical Science, which really supports the further development of Life progression.
 
Last edited:
doronshadmi said:
Let's look at this phrase: "Not all things that share one property (e.g. being a circle) have all the same other properties."

It is true, but there are properties that if they are not related to a given thing it can't be considered as this thing anymore, for example:

1. An empty set that has more than 0 members.
Click to expand...

Umm, the definition of "empty set" excludes the possibility of there being any members. As an expository example, your statement has no value.

2. A circle without Pi.
Click to expand...

Pi plays no role whatsoever in the definition of circles, just like division plays no role whatsoever in the definition of integers. You statement, here, is profoundly ignorant.

You really have trouble separating definition from axiom from theorem, don't you? You should work on that...and logic...and reading comprehension...and....

...<mindless babbling mercifully snipped>...
Click to expand...
 
Point = Circle by anyone who claims that "Pi plays no role whatsoever in the definition of circles".
 
doronshadmi said:
Point = Circle by anyone who claims that "Pi plays no role whatsoever in the definition of circles".
Click to expand...

You have provided yet another example of your comprehension and reasoning difficulties, Doron. Actually, three examples all in one sentence. Well, done!
 
doronshadmi said:
2. A circle without Pi.
Click to expand...

I see that the culinary art of Organic Mathematics can't just do without that particular ingredient.

Your mind cannot free itself from the notion popular in the past ages when most folks were linking number zero with non-existence. (See expression Anno Domini.). But that's not what that symbol stands for. If there is zero apples in a fruit basket, it doesn't mean that apples don't exist. You are refusing to accept the existence of a dress that no one can fit in. (Why would anyone make such a dress?) But such a dress does exist, and I will stitch it for you.

If C = 2r*pi = 0, then r = 0, and circumference C of the circle is zero.

The zero circumference is the dress, but no circle can wear it. That's because

y = √(02 - x2)

doesn't return a real result.

But that y can exist in the form z = a + bi, which is a complex number/textile made of the real part a and the imaginary part b. But unlike in the movies where you can see stuff that actually doesn't exist, you can't see the circle drawn on the complex plane, because that plane is reserved for plotting complex numbers and not for drawing points according to various functions.

Your expression "valid circle" comes from a term called "invalid division by zero." You were thinking... If the circumference of a circle is zero and the radius equals zero as well, then "Pi cannot be found," because

Circumference/2*Radius = Pi

So if Circumference = 0 and 2*Radius = 0, then

0/0 = "invalid operation (division by zero)"

The problem is that the Gospel of Peano includes an axiom that says

a*0 = 0

You can use the axiom to check the correctness of a division result that says

If a/b = c, then c*b = a

and so

If Circumference/Diameter = Pi, and C=0, D=0, then 0/0 = Pi with Pi * 0 = 0.

and Pi has been found. Wrap your head around it...
 
Last edited:
doronshadmi said:
Point = Circle by anyone who claims that "Pi plays no role whatsoever in the definition of circles".
Click to expand...
You should be more specific and justify your claim, because Pi doesn't really figure in the definition of the circle. The following definition comes from Wikipedia:
A circle is a simple shape of Euclidean geometry that is the set of points in the plane that are equidistant from a given point, the centre. The distance between any of the points and the centre is called the radius.
Click to expand...
No sign of Pi.

For Pi to exist in relation to a circle, the circle has to be drawn first, but Pi is hardly instrumental in the process. If the drawing is done by a compass, then radius is the important parameter and it is included in the definition. When it is a function that draws the circle, radius is again included among the variables, but not Pi. Can you reveal a method that utilizes Pi for drawing/defining a circle?
 
Status
Not open for further replies.

Back
Top Bottom