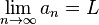The word "power" here is not defined and is not a commonly accepted mathematical term.
I disagree with you because:
1) The word "power" is a commonly accepted mathematical term (please look at the links that are related to mathematics in
https://www.google.co.il/#q="the+po...09,d.d2k&fp=5e2f9d156cef3961&biw=1272&bih=631 )
2) I use the term "power of the continuum" as a property which is related to a given non-composed dimensional space > 0, w.r.t any possible amount of lower non-composed dimensional spaces or sub-spaces (which are mixed (and therefore) composed results of several non-composed dimensional spaces) on it.
I have defined infinity as a symbol representing growing without bound. It has nothing to do with "collection."
"Growing without bound" is exactly the inability of infinitely many lower non-composed dimensional spaces and/or sub-spaces (as described above) to reach the non-locality of a given higher dimensional space (which is not necessarily a metric space). In other words, infinitely many objects can't be but unbounded collections.
Your argument is circular because it references itself. You state that spaces cannot be "composed" of lower dimensional subspaces. You then state that the power of infinity is determined by the space, which means that spaces cannot be "composed" of lower dimensional subspaces.
Each one of k-dimensional spaces (such that k = 0 to infinite amounts) is non-composed, but the relations among k-dimensional spaces under an arbitrary higher k-dimensional space > 0, provide collections of non-composed elements and\or composed objects, where no amount of lower non-composed dimensional spaces and\or composed objects of such collections, has the power of infinity of the given higher k-dimensional space > 0.
Your definition of infinity is non-existent.
I is your true as long as you get it only in terms of collections with unbounded amount of members (without the understanding of why they growing without bound (exactly because they can't reach the power of infinity (the non-composed state) of a given higher (non-composed) k-dimensional space (which is not necessarily a metric space).
You talk about what it does, not what it is.
Wrong, I clearly talk about the non-locality of a given higher (non-composed) k-dimensional space (which is not necessarily a metric space), that can't be reached by any given amount of lower non-composed dimensional spaces and\or composed objects, on it.
You aren't proving anything.
No the contrary, I provide the reasoning to understand why infinity in terms of collections is essentially unbounded or, in your own words, "growing without bound" (as I show above).
You just state things like "non-composed dimensional space" without any framework. You have to make these terms exact and understandable by the rest of us before we are going to care about them.
Wrong, I clearly provide verbal_symbolic
AND visual_spatial framework, which enables to deal with things like "non-composed dimensional space ≥ 0".
It is clearly not the traditional reasoning, which is derived only from verbal_symbolic brain skills of the discussed subject (this traditional reasoning is clearly seen by your own following words: "I have defined infinity as
a symbol representing growing without bound" (in other words, no visual_spatial brain skills are also used by you in order to define infinity).
You have to make these terms exact and understandable by the rest of us before we are going to care about them.
You have to used also your visual_spatial brain skills of the discussed subject, if you which to understand terms that are defined exactly by using verbal_symbolic AND visual_spatial brain skills. (since when your under totally depends.
... understandable by the rest of us before we are going to care about them.
In other words, you ask for a reasoning that is derived from using verbal_symbolic
AND visual_spatial brain skills, to be expressed only by verbal_symbolic brain skills (of the discussed subjects).
Please free your mind by let it go beyond verbal_symbolic brain skills (of the discussed subjects).
If you do that we are in the first stage in order to develop some communication between us.