Interesting how your argument shifts. First you didn't understand what self-similarity even meant, and now you are about to redefine it in order to bend reality to cover your blunders.
The generally accepted characteristics required of a fractal are (1) self-similarity, (2) nowhere differentiability, and (3) having a fractal dimension (which is a measure of change in complexity with scale).
Your diminishing staircase meets exactly none of those characteristics.
The term, fractal, has become widely abused, probably due to fractals' inroads into popular culture via their influence in art and especially computer animation. Many things get called fractals even though there are not.
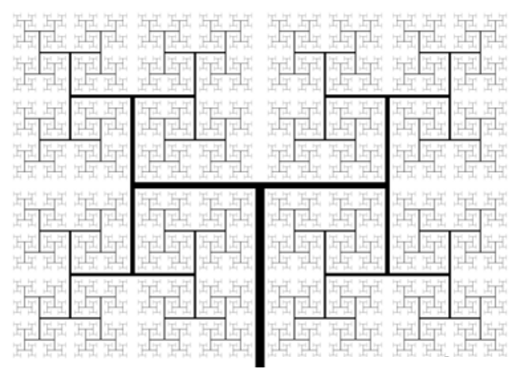
For example, this is not:
http://fishofthebay.com/wp-content/themes/fishofthebay/images/fractal.png
Well, it is known as H-fractal (as can be found in
http://en.wikipedia.org/wiki/H-fractal or
http://en.wikipedia.org/wiki/List_of_fractals_by_Hausdorff_dimension ) and it is arbitrarily close to Hausdorff dimension 2.
So we can ignore your "understanding" of fractals, which does not able to capture that the place-value method is actually a fractal.
Since you do not understand what fractals are, you are also unable to capture
http://www.internationalskeptics.com/forums/showpost.php?p=9330591&postcount=2586.
Probably you will claim that since (according to Standard Mathematics) it has Hausdorff dimension 2, it means that a collection of lower dimensional spaces can completely cover a higher dimensional space.
But then we return to stage one, where I
axiomatically claim (by using verbal_symbolic AND visual_spatial reasoning) that collections of lower dimensional spaces are not extensible into a non-composed higher dimensional space, and a non-composed higher dimensional space is irreducible into lower dimensional spaces.
One of the results of this axiomatic approach is that 1 > 0.999... , but know I carefully have to check how to consistently express this inequality also by verbal_symbolic reasoning.
-----------------
Before I continue, I which to clarify some things.
During my work I make mistakes, where my last mistake was that I did not carefully checked the following expressions, which are wrong
1 - 9/9 = 0/9 = 0
1 - 8/9 = 1/9 > 0.1111 ... by 0.000...9
10
1 - 7/9 = 2/9 > 0.2222 ... by 0.000...8
10
1 - 6/9 = 3/9 > 0.3333 ... by 0.000...7
10
1 - 5/9 = 4/9 > 0.4444 ... by 0.000...6
10
1 - 4/9 = 5/9 > 0.5555 ... by 0.000...5
10
1 - 3/9 = 6/9 > 0.6666 ... by 0.000...4
10
1 - 2/9 = 7/9 > 0.7777 ... by 0.000...3
10
1 - 1/9 = 8/9 > 0.8888 ... by 0.000...2
10
1 - 0/9 = 9/9 > 0.9999 ... by 0.000...1
10
as shown by jsfisher, by using the expression 9*(1/9) = 9*(0.111..
10+0.000...9
10), which leads to inconstancy (x can't be both 0.000...1
10 AND 0.000...81
10).
I stupidly tried to defend my argument by using nonsense like inverse proportionality among two given expressions.
But then I have noticed that I made a fundamental mistake, which is: to use only verbal_symbolic reasoning, in order to deal with the expressions above.
By using also visual_spatial reasoning ( as can be seen in
http://www.internationalskeptics.com/forums/showpost.php?p=9328458&postcount=2559 ) I have found that the expressions above are actually relations among different bases, so at this stage I am working to define the right way to express these relations consistently also by verbal_symbolic reasoning.
I hope that I have learned my lesson, so from now on I am going to check my expressions by using not less than verbal_symbolic AND visual_spatial reasoning, which is, after all, my fundamental claim about any mathematical development.