By using Traditional Math I wish to see how some amount of such units define an invariant distance like pi along the real line (be aware of the fact that pi*0unit = 0 distance, or in other words, the invariant distance of pi along the real line is eliminated by 0unit, which is the absolute unit measurement that is derived from ∞ curvature.
"Traditional math" can only answer questions who are structurally sound, so you can wish indefinitely.
You should brush up on the difference between global absence and local absence. If fruit called apples doesn't exist, then apples won't appear in the basket; if they do exist, it doesn't mean that they will be placed in some particular basket.
You've been clearly struggling with something that comes to most folks naturally. So even if traditional math makes some attempt to repair your question so it could be considered, you won't be able to see the change that has been made. If you fail to understand that length, volume, area, pressure, energy, charge and so on have a unit of measurement, but ratio doesn't
then
pi = circumference/diameter = "dimensionless quantity"
You misapplied the term in your scheme, coz the initial subject never called for bringing dimensionless quantities into the picture. The subject was your previous claim that 1-dim object, such as circle, cannot be reduced to a 0-dim object, which is point. Now you vehemently argue that when radius=0, circle becomes point. Since you don't have the type of writing instrument that math uses all the time, you won't be able to prove either case through comprehensive presentation apart from the usual verbal declarations studded with phantasmagorical syntax.
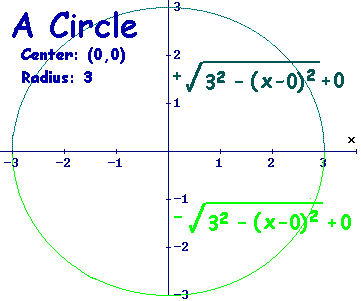
You used once the implicit equation for unit circle; that is
y
2 + x
2 = 1
but you never understood its meaning, otherwise you would be able to trace the case when r is reduced to 0 and prove the result.
How do we call the folks who take incessantly an issue with a subject without being able to understand it?
(doron s. with a single replacement.)
Since the devil has so much on his mind, then you keep going . . .